Sistema diédrico: representación del plano
1. Conceptos básicos
Un plano es una superficie plana ilimitada, sin espesor.
El plano es uno de los elementos geométricos básicos.
Tiene dos dimensiones planas (X e Y) y se puede definir de varias formas :
- Tres puntos no alineados definen un plano.
- Un punto y una recta exterior al punto definen un plano.
- Dos rectas paralelas o dos rectas que se cortan también definen un plano.
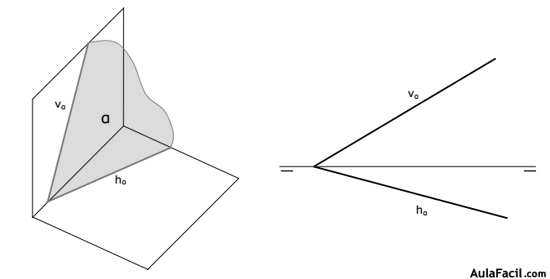
Un plano no tiene proyección (la proyección de los infinitos puntos que lo componen daría como resultado una mancha de puntos), por este motivo los planos se representan en el sistema diédrico por sus trazas.
Todo plano en el espacio del sistema diédrico genera automáticamente dos trazas en forma de dos rectas contenidas en los dos planos proyectantes. Una traza vertical, en el plano de proyección vertical, y otra traza horizontal, en el plano de proyección horizontal.
Si tenemos las trazas de dos rectas que se cortan o que son paralelas, podemos conseguir las trazas del plano definido por dichas rectas uniendo sus trazas homónimas, esto es, por un lado las trazas verticales y por otro lado las trazas horizontales de las dos rectas.
Las trazas de un plano dispuesto sin ninguna condición especial se cortan en un mismo punto de la línea de tierra.
Un plano en el espacio se marca con una letra griega mayúscula (α, β,…).
A la traza vertical de un plano se le denomina con la letra minúscula v y el subíndice α (u otra letra griega que define el plano) y a la traza horizontal de un plano se le denomina con la letra minúscula h y el mismo subíndice α (o la letra griega que le corresponda).
2. Sistemas para definir planos
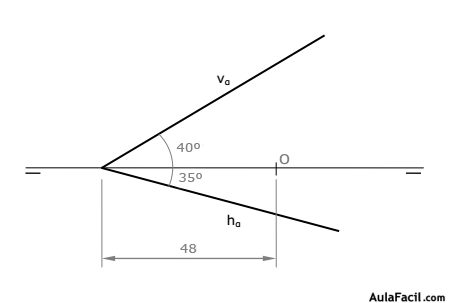
Hay varios sistemas uno de ellos es definir las características geométricas de sus trazas.
Por ejemplo: dibujar el plano α, cuya traza vertical forma 40º con LT y cuya traza horizontal forma 35º con LT, cortándose ambas en el punto A (-48, 0, 0).
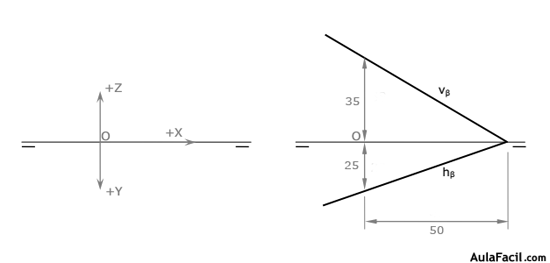
Otro sistema, más práctico y sencillo, es definir el plano por tres puntos relacionados todos con un origen de coordenadas pertenecientes siempre a LT, PH y PV, y en este mismo orden. Al ser puntos especiales, es suficiente con dar sus medidas principales X, Y, Z.
Por ejemplo: dibujar el plano β (47,29, 38)
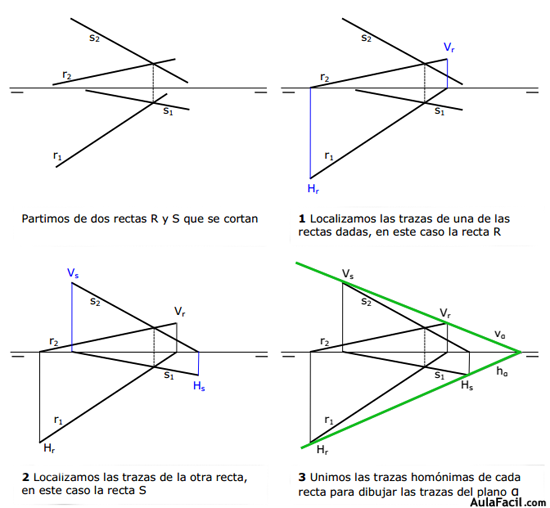
3. Plano definido por dos rectas que se cortan
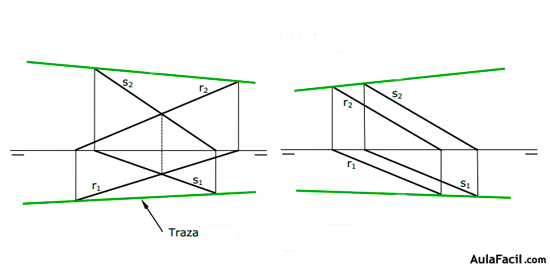
Ya hemos comentado que dos rectas que se cortan definen un plano. También sabemos que dos rectas que se cortan tienen un punto común.
En la figura siguiente se puede ver cómo se dibuja un plano definido por dos rectas que se cortan, dibujando las trazas del plano por las trazas homónimas de las rectas dadas.
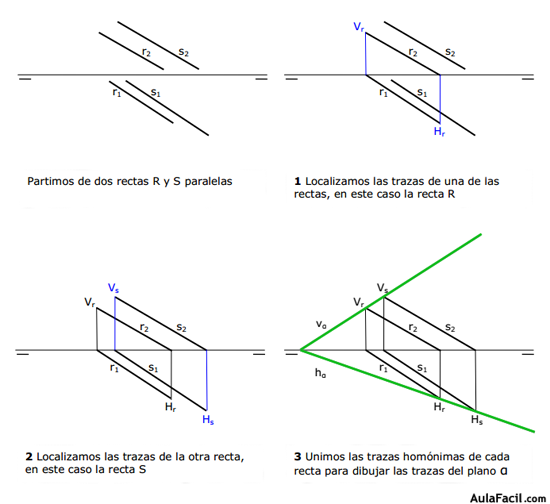
4. Plano definido por dos rectas paralelas
Ya hemos comentado que dos rectas paralelas definen un plano. También sabemos que dos rectas paralelas tienen sus proyecciones paralelas.
En la figura siguiente se puede ver cómo se dibuja un plano definido por dos rectas paralelas, dibujando las trazas del plano por las trazas homónimas de las rectas dadas.
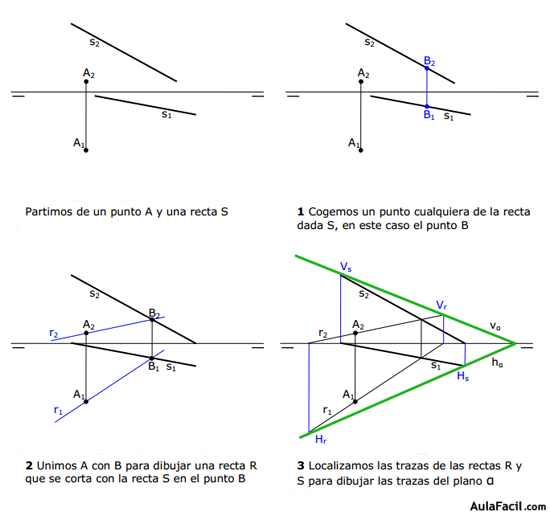
5. Plano definido por una recta y un punto
Una recta y un punto exterior a ella definen un plano. Para dibujar el plano que forman una recta y un punto debemos coger un punto cualquiera de la recta y trazar la recta que definen el punto dado y el punto que hemos elegido en la recta, lo que da lugar a dibujar un plano definido por dos rectas que se cortan, que ya sabemos cómo se hace.
En la figura siguiente se puede ver cómo se dibuja un plano definido por una recta y un punto exterior a ella.
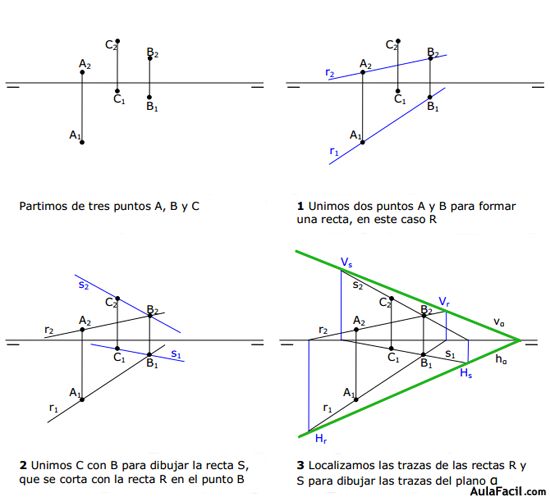
6. Plano definido por tres puntos
Tres puntos no alineados definen un plano.
Para dibujar el plano que forman tres puntos no alineados debemos unir los tres puntos, dos a dos, para tener dos rectas que se cortan en uno de ellos, lo que da lugar a dibujar un plano definido por dos rectas que se cortan, que ya sabemos cómo se hace.
En la figura siguiente se puede ver cómo se dibuja un plano definido por tres puntos no alineados.
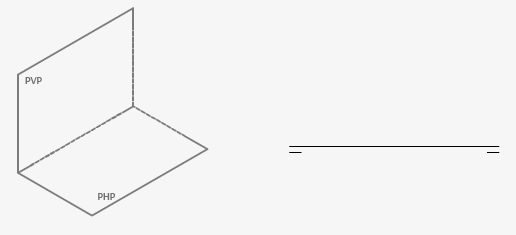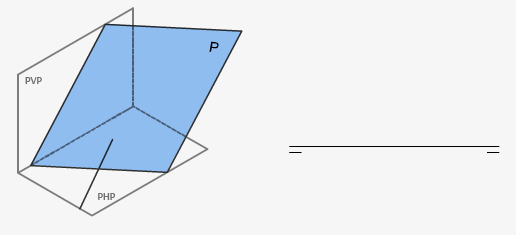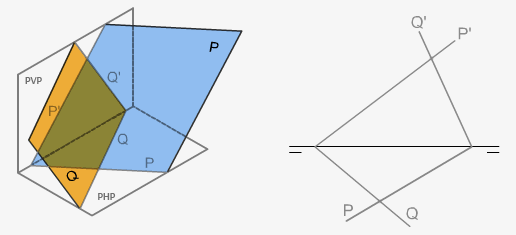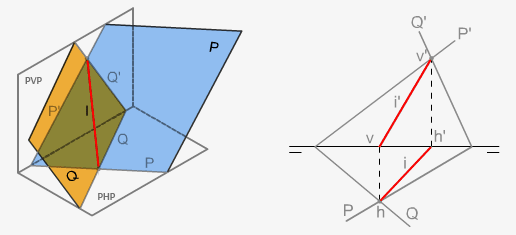
7. Intersección de dos planos (método general)
Para hallar la intersección de dos planos dados hallamos los puntos de corte de sus trazas que nos determinará la recta de intersección que pasa por esos dos puntos.