Tangencias entre rectas y circunferencias

1. Recta tangente a una circunferencia

1.1 Desde un punto exterior

Lo resolvemos uniendo el punto P con el centro de la circunferencia, hallamos el centro del segmento PO y trazamos una circunferencia que pase por los extremos, cortando en T1 y T2, que son los puntos que forman el arco capaz de 90º del segmento PO.

1.2 Por un punto de la curva

Unimos el punto T con el centro de la circunferencia y trazamos la recta perpendicular al radio por ese punto.

1.3 Paralela a una dirección dada

Trazamos la perpendicular por el centro de la circunferencia a la recta r y hallamos el punto T1, que es el punto tangente a la circunferencia de la recta s paralela a r

2. Circunferencia tangente a una recta

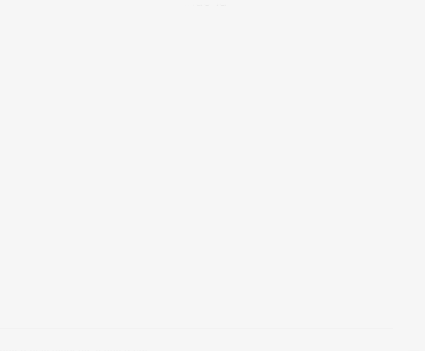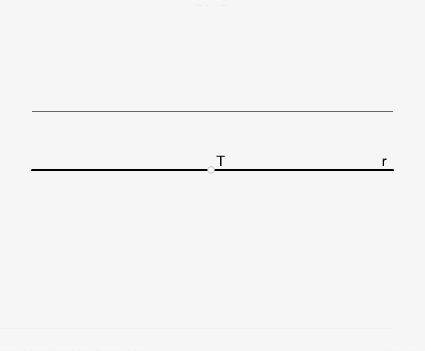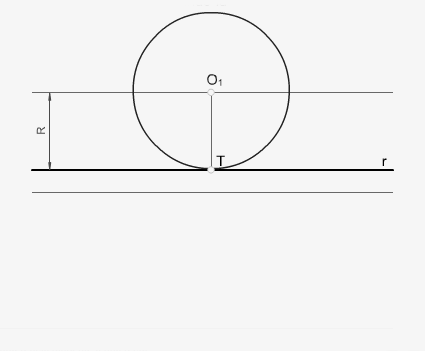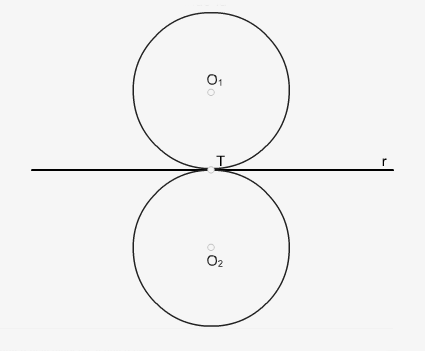
2.1 Conocido el punto de tangencia en la recta y el radio de tangencia

Trazamos el radio perpendicular a la recta r por el punto de tangencia T y dibujamos la circunferencia.

2.2 Conocido el radio de tangencia y que pase por un punto exterior

Trazamos una paralela a la recta r con una distancia igual al radio R y desde P trazamos un arco con radio R que corte a la paralela. Los puntos de corte O1 y O2 son los centros de las circunferencias tangentes a r que pasan por el punto P.