Transformaciones geométricasan anamórficas
Son aquellas en las que cambia la forma entre la original y la transformada.
Podemos distinguir tres tipos de transformación:
1. Homología
La homología es una transformación que no es isomórfica ni isométrica, pues no mantiene la forma ni el tamaño de las figuras. Transforma los puntos del plano A, B, C… en puntos del plano A’, B’, C’... de modo que:
- Dos puntos homólogos A y A’ están alineados con un punto fijo O que es el centro de la homología.
- Dos rectas homólogas r y r’ se cortan en una recta llamada eje de homología.

2. Afinidad
La afinidad es una homología con el centro en el infinito. Es una transformación que no es isomórfica ni isométrica, pues no mantiene la forma ni el tamaño de la figura que transforma.
Transforma los puntos del plano A, B, C… en puntos del plano A’, B’, C’... de modo que:
- Dos puntos homólogos A y A’ definen un segmento paralelo a la dirección de afinidad d.
- Dos rectas homólogas r y r’ se cortan en una recta llamada eje de afinidad.

3. Inversión
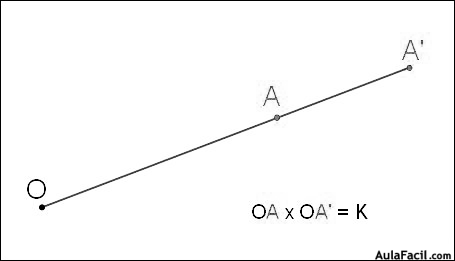
La inversión es una transformación que hace corresponder a un punto A otro punto A’ cumpliendo las siguientes condiciones:
- Ambos puntos están alineados con otro punto fijo O, llamado centro de inversión.
- El producto de las distancias de ambos puntos al citado centro de inversión es un valor constante K llamado potencia de inversión, es decir; OA x OA’=K