Curvas cíclicas: trazado del hipocicloide

1. Curva hipocicloide

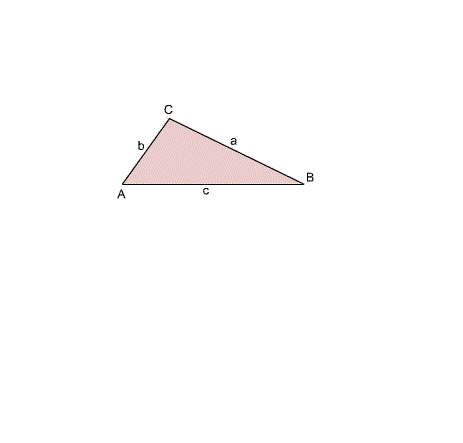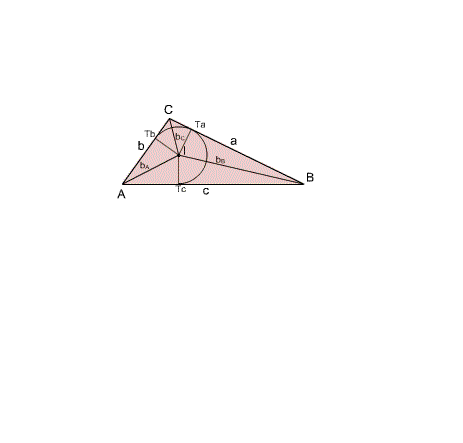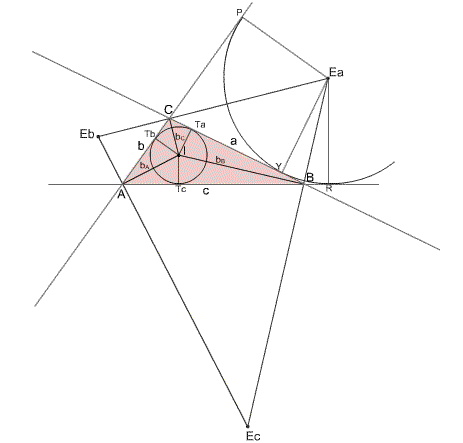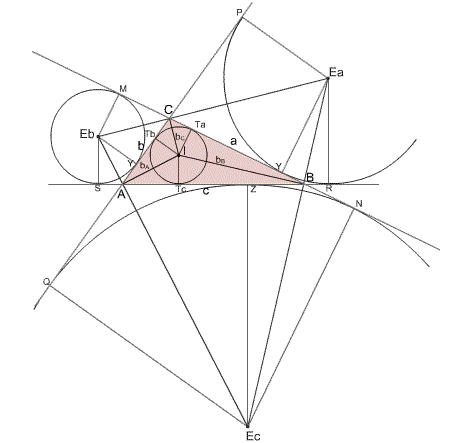
Una curva hipocicloide es la trayectoria descrita por un punto situado sobre una circunferencia generatriz que rueda sin deslizarse por el interior de otra circunferencia directriz.

2. Trazado

1. Dividimos la circunferencia (ruleta) de centro O y radio conocido en n partes iguales; en nuestro ejemplo 8 partes.
2. Desde O' (origen de la directriz) trazamos semicircunferencias por los puntos divisorios de nuestra ruleta.
3. Dividimos el perímetro de la semicircunferencia que hace de directriz en el doble de partes que la ruleta, 16 divisiones, y trazamos líneas desde O' hasta los puntos de corte.
4. Desde las intersecciones con la semicircunferencia de origen O' que pasa por O, trazamos círculos con diámetro igual al de nuestra ruleta y marcamos los puntos (desde el extremo del diámetro de la directriz) que cortan con las demás semicircunferencias, en orden y consecutivamente.
5. Unimos los puntos a mano alzada y dibujamos la curva hipocicloide.