Curvas cónicas: generalidades
1. Definición y propiedades
Se llaman curvas cónicas a todas aquellas que se obtienen cortando un cono con un plano. Debido a su origen, las curvas cónicas se llaman a veces secciones cónicas.
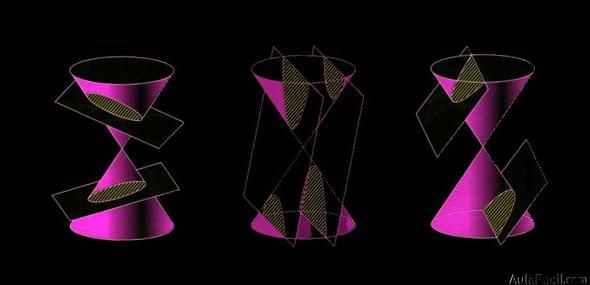
- Las elipses son las curvas que se obtiene cortando una superficie cónica con un plano que no es paralelo a ninguna de sus generatrices.
- Las hipérbolas son las curvas que se obtiene al cortar una superficie cónica con un plano que es paralelo a dos de sus generatrices (base y arista).
- Las parábolas son las curvas que se obtienen al cortar una superficie cónica con un plano paralelo a una sola generatriz (arista).
2. Elementos
- Eje de simetría: rectas imaginarias que dividen a la curva en dos partes simétricas.
- Eje real: es el segmento que pasa por los focos y corta a la curva cónica en dos puntos (V1, V2).
- Focos: punto o puntos fijos (F1, F2) de una curva respecto de los cuales se mantienen constantes las distancias relacionadas con los puntos de dicha curva.
- Radio vector: segmento que une cualquier punto de la curva con su foco correspondiente (P, F2).
- Directrices: es la recta que pasa por los puntos de intersección de la recta tangente a las dos esferas inscritas y las rectas formadas por las tangentes de las esferas con el cono.
- Circunferencia principal: tiene su centro en la mitad de su eje real y su diámetro es igual al eje real (V1, V2).
- Circunferencias focales: tienen sus centros en los focos y su diámetro es el eje real.
- Exentricidad: es un parámetro que determina el grado de desviación de una sección cónica con respecto a una circunferencia.