La hipérbola: definición y propiedades

1. La hipérbola

La hipérbola es el lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos fijos llamados focos es constante e igual a la distancia entre ellos.

Los tres parámetros que definen una hipérbola son :

1. Eje real AA’: o principal.

2. Eje imaginario CD: o secundario, es perpendicular al eje real.

3. Focos: puntos fijos sobre el eje AA’, de referencia de distancias

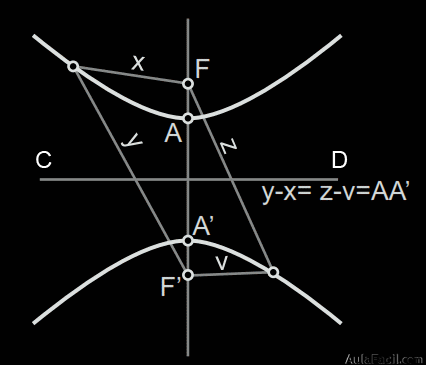
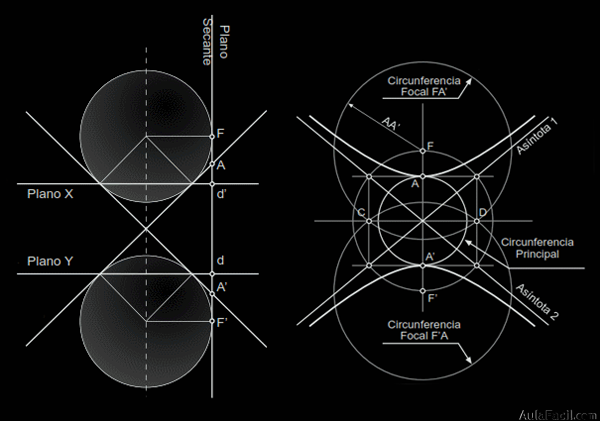
2. Elementos que intervienen (teorema de Dandelin)

1. Plano secante a todas las generatrices menos a dos con las que son paralelas (circunferencias focales).

2. Hipérbola: curva plana y abierta de dos ramas que el plano secante produce al cortar las generatrices del cono.

3. Esferas tangentes al cono de revolución y al plano secante.

4. Eje real (focal o transverso): recta que pasa por los focos. Distancia de un vértice (A) al otro (A’).

5. Focos: puntos F y F’ de tangencia de las esferas con el plano secante.

6. Radios vectores son dos segmentos que parten de los focos a un mismo punto de la hipérbola.

7. Planos X e Y: planos que pasan por los puntos de tangencia de cada esfera con el cono.

8. Directrices: rectas de intersección de los planos X Y con el plano secante.

9. Asíntotas: dos rectas que son tangentes en el infinito a los extremos de las ramas (impropios).

10. Excentricidad es la razón constante, para todos los puntos de la hipérbola, de distancias de un punto de la cónica a un foco y a su directriz. “Es el achatamiento de la hipérbola” y viene marcada por el distanciamiento entre sus dos focos. Cuanto más alejados estén los focos entre sí más excéntrica será la hipérbola