La parábola: definición y propiedades

1. La parábola

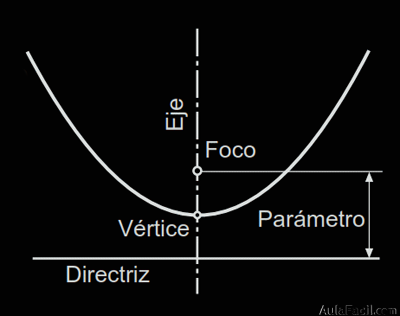
La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y una recta llamada directriz.

Los tres parámetros que definen una parábola son:

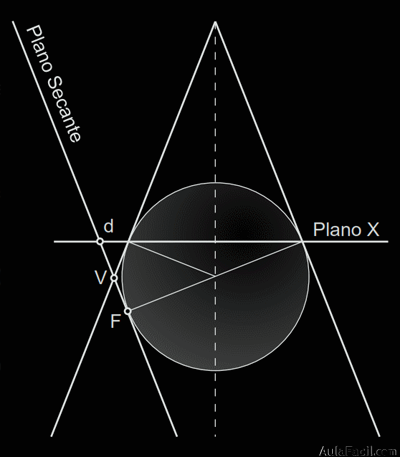
1. Foco F: punto de tangencia de la esfera (tangente al cono) con el plano secante.

2. Directriz d: recta intersección del plano X con el plano secante. Perpendicular al eje de simetría.

3. Vértice A: vértice extremo del eje, y por tanto de la curva. Se encuentra en el punto medio entre el foco y la directriz.

2. Elementos que intervienen (teorema de Dandelin)

1. Plano secante a todas las generatrices del cono menos a una de ellas al que es paralelo.

2. Parábola: curva plana y abierta de una sola rama.

3. Esfera tangente: al cono de revolución y al plano secante.

4. Radio Vectores: segmentos que parten del foco a un punto perteneciente a la parábola, y de éste perpendicular a la directriz.

5. Foco: punto F de tangencia de la esfera con el plano secante.

6. Plano X: planos que pasan por (contienen) los puntos (circunferencia) de tangencia de la esfera tangente con el cono y el plano secante.

7. Directriz: recta intersección del planos X con el plano secante.

8. Eje: recta que pasa por el foco y se extiende entre los dos vértices, V y V’ (impropio, en el infinito). Es eje de simetría de la curva y es perpendicular a la directriz.