Aplicación de integrales en el movimiento rectilíneo
Sabemos que la operación contraria a la derivación es la integración lo que nos permite calcular la posición de un móvil a partir de la expresión de su aceleración en un momento dado.
Es algo parecido a la “marcha atrás” en el caso de que la “marcha adelante” fuera producida por las derivadas.
Partimos de  y queremos obtener la que se deriva de ésta cuando
y queremos obtener la que se deriva de ésta cuando 
Simplemente hallamos su derivada tal como lo hemos hecho en el último ejercicio:  .
.
¿Podemos hacer lo contrario, es decir, nos dan la que se ha derivado o emanado o resultado y nos piden que hallemos la anterior, la primitiva?
La anterior, la primera, la primitiva de  , es como decir, la expresión de donde procede ésta la obtenemos por medio de la integración (no olvides de que v está en función de t):
, es como decir, la expresión de donde procede ésta la obtenemos por medio de la integración (no olvides de que v está en función de t):
Sabemos que:

Haciendo operaciones….
Como  sustituimos en la igualdad anterior quedándonos:
sustituimos en la igualdad anterior quedándonos: 
Integramos ambos miembros de la igualdad:
Al integrar el primer miembro de la igualdad nos encontramos con la derivada de e, al ser operaciones contrarias la derivación y la integración, se “simplifican” o si quieres se “anulan”. Sería como si a 3 le multiplicaras y dividieras por 5, por tanto, nos queda:

Esta igualdad la podemos escribir:

Sacamos fuera del signo integral a las constantes:

Hallando las integrales obtenemos:

Esta sería una solución general.
C puede tener cualquier valor que pertenezca a porque a la hora de derivar su valor equivale a cero por tratarse de una constante.
Para saber el valor concreto de C, en el enunciado nos deben proporcionar algún dato que nos permita su cálculo.
En nuestro caso concreto podrían habernos dicho que su representación gráfica pasa por el punto (1,6):

Tienes en azul la representación gráfica de la función de:

1.79 Anteriormente dedujimos que  Después de lo estudiado hasta aquí ¿podrías demostrar, partiendo de la aceleración y utilizando integrales llegar a esta expresión, paso a paso?
Después de lo estudiado hasta aquí ¿podrías demostrar, partiendo de la aceleración y utilizando integrales llegar a esta expresión, paso a paso?
Respuesta: La respuesta incluye la explicación siguiente:
Partimos de que 
Despejamos 
La aceleración es una constante (movimiento rectilíneo uniformemente acelerado).
Hallamos integrales en ambos miembros de la última igualdad:

En el primer miembro de la última igualdad la integral con la derivada de la velocidad simplificamos.
Del segundo miembro sacamos fuera de la integral a la constante, en este caso, la aceleración:

Resolvemos la integral quedándonos:
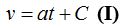
Supongamos que en el momento 0 cuando el móvil comienza su movimiento lleva una velocidad v0, es decir, v= vo (en el momento t0 ) sustituimos estos valores en v= at + C y obtenemos:

Comprobamos que C= vo
Sustituimos el valor de C en (I) obteniendo: v= vo + at (II)
Sabemos que  y de esta expresión despejamos la derivada de e:
y de esta expresión despejamos la derivada de e:

Hallamos integrales en ambos miembros de la última igualdad:

La integral con la derivada del espacio se anulan y en el segundo miembro sustituimos el valor de v por su valor hallado en (II):

Quitamos paréntesis dentro del integrando:

A los factores que no dependen de t al considerarles constantes los sacamos del integrando:

Integramos la última igualdad:

Para hallar el valor de C debemos tener en cuenta que al comienzo del movimiento el tiempo transcurrido es 0 y eo el espacio recorrido por lo que:

Se nos convierte en:

Por lo que al final nos queda ordenando:

Donde eo en la fórmula final indica la posición que ocupaba el móvil antes de comenzar el movimiento.
Este dato no se tiene en cuenta mientras no se indique en el enunciado.
