Cálculo de la aceleración tangencial
La aceleración tangencial (at) relaciona la variación de la rapidez con el tiempo.
En el momento de ver en el velocímetro la rapidez del coche al paso por dos puntos de su trayectoria, nos está dando el módulo de la velocidad independientemente que se trate de una recta o una curva el camino que está recorriendo.
Esto te permite aplicar la fórmula ya conocida 
de donde 
.
1.104 Un móvil con velocidad uniformemente acelerada describe una circunferencia de 3 m de radio. Al pasar por un punto Po de su trayectoria circular es de 20 m/s y en otro punto P1 después de 0,5 segundos es de 30 m/s. ¿Cuál es su aceleración tangencial?
Respuesta: 20 m/s2
Solución.
Aplicamos lo que acabamos de indicar:
Disminución de la rapidez:
La rapidez puede ser disminuida, es decir, podemos producir una aceleración negativa sirviéndonos del freno:
Otro modo de abordar el cálculo de la aceleración tangencial:
La aceleración tangencial se refiere a la variación de la rapidez con relación al tiempo como hemos dicho anteriormente y podemos escribir:
La derivada de la velocidad con relación al tiempo cuando el incremento de éste tiende a 0 nos dará la aceleración.
Sabemos que el módulo del vector de la velocidad lineal o tangencial v equivale a 
.
R es una constante por lo que podremos escribir en función de la aceleración angular α que la estudiamos anteriormente:
Este resultado lo expresamos en radianes por segundo cuadrado.
1.105 Un tiovivo de 3m de radio está girando, como es de suponer, con una velocidad angular constante. ¿Puedes calcular la aceleración tangencial del “caballito” situado al borde de la plataforma giratoria?
Respuesta: No tiene aceleración tangencial.
Solución.
Sabemos que 
y mientras gira el tiovivo las dos velocidades del numerador son iguales y sucederá:
Por lo que 
1.106 Un móvil sigue una trayectoria circular de 3 m de radio y conocemos que el ángulo descrito, en función del tiempo, nos viene dada por la ecuación 
Calcula la velocidad angular y la aceleración tangencial en el instante que haya transcurrido 1 segundo.
Respuestas: 1ª) 16 rad/s; 2ª) 84 m/s2
Solución.
Sabemos que a partir de la ecuación correspondiente al espacio, en función del tiempo, y cuando éste tiende a cero, su primera derivada equivale a la velocidad y la que se deriva de ésta, corresponde al valor de la aceleración.
La velocidad angular será la primera derivada:
La aceleración angular es la derivada de la velocidad angular en función del tiempo:
La aceleración tangencial es:
En ambos casos, el tiempo equivale a 1 segundo.
1.107 En una trayectoria circular de 30 cm de radio, un móvil, (partiendo del origen) la recorre con una aceleración tangencial correspondiente a la ecuación a = 40t.
Calcula la aceleración tangencial al cabo de 1 segundo y su velocidad tangencial al cabo de ese tiempo.
Respuestas: 1ª) 40 m/s2 ; 2ª) 20 m/s
Solución.
Para la aceleración tangencial basta sustituir a t por 1:
Para la velocidad tangencial utilizamos integrales. La “anterior” (primitiva) a la aceleración es la velocidad:
Como parte del origen C vale 0 y si t vale 1: v = 20 m/s
1.108 Un móvil se desplaza por un circuito circular a 72 km/h con una frecuencia de 4 hercios.
Calcula la velocidad angular de las ruedas y el radio de cada una sabiendo que todas son iguales.
Respuestas: 1ª) 25,13 rad/s; 2ª) 0,8 m
Solución.
La velocidad tangencial 72 km/h la reducimos a m/s:
Vueltas por segundo llamamos hercio.
La velocidad angular que nos viene dada en radianes por unidad de tiempo y equivale a la velocidad de rotación es, en nuestro caso por segundo:
Sabemos que 
y sustituyendo valores conocidos y despejando R tendremos:
1.109 Si la Tierra tiene un radio de 6300 km, desde su centro al lugar donde está situado el país K ¿cuáles son su velocidad angular y la velocidad tangencial relativas a este país, en rad/s y m/s?
Respuestas: 1ª) 0,000073 rad/s ;2ª) 460 m/s
Solución.
Como la Tierra da una vuelta cada 24 horas su velocidad angular por hora es:
La velocidad tangencial en el país K es, sustituyendo valores conocidos:
1.110 Tenemos una pista circular de 200 m de radio ¿cuál es la velocidad constante angular y la aceleración tangencial de un móvil que realiza 40 vueltas en 1 hora?
Respuestas: 1ª) 0,07 rad/s; 2ª) 0
Solución.
Las 40 vueltas en 1 hora equivalen a:
Si la velocidad angular es constante significa que α (su aceleración angular) vale 0 porque si tomas el valor de esta velocidad en un momento y es 123 rad/s y vuelves a tomar 3 segundos después, como la velocidad angular se mantiene constante veremos que es 123 rad/s. La diferencia entre las velocidades angulares inicial y final será 0 lo que nos indica que su aceleración α vale 0.
La aceleración tangencial equivale a: 
1.111 Un volante de inercia de 50 cm de radio partiendo del reposo se pone en marcha necesitando 20 segundos en alcanzar la velocidad necesaria, que después la mantiene, contando con una aceleración angular, durante este tiempo, de 40 rad/s2.
Calcula:
1) La velocidad del volante después de 20 segundos.
3) Las vueltas que ha dado durante los primeros 20 s.
4) La aceleración tangencial después de 1 minuto de haber arrancado.
Respuestas: 1ª) 800 rad/s; 2ª) 7639,44 rpm; 3ª) 1273,24 vueltas; 4ª) at =0
Solución.
1ª) Sabemos que 
y en este caso la velocidad angular inicial vale 0 porque parte del reposo.
Sustituyendo valores conocidos: 
2ª) Los 800 rad/s expresamos en rpm:
Radianes por minuto: 
Cada vuelta completa equivale a 
radianes, luego el número de giros en 1 minuto será:
3ª) Calculamos el ángulo total recorrido durante 20 s y sustituimos los valores que conocemos:
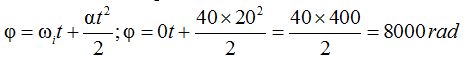
Si cada vuelta equivale a 2π radianes el número de vueltas será:
4ª) Lo explicado en el ejercicio anterior respecto a la aceleración tangencial lo aplicas en éste.
Al tener velocidad angular constante α vale cero que al multiplicar por el radio será 0 también el resultado.
