Comportamiento de la amplitud del ángulo en cuanto a la duración del tiempo del móvil en el espacio
La respuesta es simple siempre que dispongas de unas Tablas Trigonométricas.
Para facilitarte el trabajo tienes a continuación los valores de los senos desde 1º hasta 90º:
GRADOS | SENO | GRADOS | SENO | GRADOS | SENO |
1 | 0,01745241 | 31 | 0,51503807 | 61 | 0,87461971 |
2 | 0,0348995 | 32 | 0,52991926 | 62 | 0,88294759 |
3 | 0,05233596 | 33 | 0,54463904 | 63 | 0,89100652 |
4 | 0,06975647 | 34 | 0,5591929 | 64 | 0,89879405 |
5 | 0,08715574 | 35 | 0,57357644 | 65 | 0,90630779 |
6 | 0,10452846 | 36 | 0,58778525 | 66 | 0,91354546 |
7 | 0,12186934 | 37 | 0,60181502 | 67 | 0,92050485 |
8 | 0,1391731 | 38 | 0,61566148 | 68 | 0,92718385 |
9 | 0,15643447 | 39 | 0,62932039 | 69 | 0,93358043 |
10 | 0,17364818 | 40 | 0,64278761 | 70 | 0,93969262 |
11 | 0,190809 | 41 | 0,65605903 | 71 | 0,94551858 |
12 | 0,20791169 | 42 | 0,66913061 | 72 | 0,95105652 |
13 | 0,22495105 | 43 | 0,68199836 | 73 | 0,95630476 |
14 | 0,2419219 | 44 | 0,69465837 | 74 | 0,9612617 |
15 | 0,25881905 | 45 | 0,70710678 | 75 | 0,96592583 |
16 | 0,27563736 | 46 | 0,7193398 | 76 | 0,97029573 |
17 | 0,2923717 | 47 | 0,7313537 | 77 | 0,97437006 |
18 | 0,30901699 | 48 | 0,74314483 | 78 | 0,9781476 |
19 | 0,32556815 | 49 | 0,75470958 | 79 | 0,98162718 |
20 | 0,34202014 | 50 | 0,76604444 | 80 | 0,98480775 |
21 | 0,35836795 | 51 | 0,77714596 | 81 | 0,98768834 |
22 | 0,37460659 | 52 | 0,78801075 | 82 | 0,99026807 |
23 | 0,39073113 | 53 | 0,79863551 | 83 | 0,99254615 |
24 | 0,40673664 | 54 | 0,80901699 | 84 | 0,9945219 |
25 | 0,42261826 | 55 | 0,81915204 | 85 | 0,9961947 |
26 | 0,43837115 | 56 | 0,82903757 | 86 | 0,99756405 |
27 | 0,4539905 | 57 | 0,83867057 | 87 | 0,99862953 |
28 | 0,46947156 | 58 | 0,8480481 | 88 | 0,99939083 |
29 | 0,48480962 | 59 | 0,8571673 | 89 | 0,9998477 |
30 | 0,5 | 60 | 0,8660254 | 90 | 1 |
Te es fácil comprobar que a medida que el ángulo crece, el valor de su seno también lo hace, por lo que el tiempo, por depender directamente de este factor también se hará mayor.
No obstante, esto tiene un límite para que la trayectoria sea parabólica. El movimiento sería vertical con 90º.
B) Distancia horizontal recorrida por el móvil o alcance
Al tratarse de la distancia horizontal nos referimos al eje de abscisas x cuya medida nos vendrá dada según el valor del tiempo que dura el movimiento, es decir: 
Sabemos que  y que el valor de t ya lo tenemos calculado anteriormente:
y que el valor de t ya lo tenemos calculado anteriormente:  pues bien, este valor lo sustituimos en (I) y hacemos operaciones:
pues bien, este valor lo sustituimos en (I) y hacemos operaciones:

Sabemos por Trigonometría que:

Si los ángulos son iguales ( a = b) tenemos:

Sustituyendo en:

Tenemos:

1.124 Supongamos que Astérix, tras un buen trago de poción mágica, se enfrenta al soldado romano de turno y tras un bofetón,

éste sale disparado a una velocidad de 900 m/s con un ángulo de 80º. ¿A qué distancia le ha enviado?
Respuesta: 28269 m
Solución.
No tienes más que aplicar la fórmula y hacer las operaciones en ella indicada:

Recuerda que los senos de 160º y 20º son iguales: 160º+20º =180º.

Observación: Parece ser que el señor Panoramix ha tenido alguna pequeña confusión en el cálculo de las proporciones.
C) Altura máxima alcanzada en su trayectoria.
Recuerda que estamos estudiando el caso en el que el movimiento parabólico se efectúa a partir de y = 0.
La altura máxima se alcanza en el momento en que la velocidad  , es decir, cuando g vale 0, tal como quedó reflejada en una gráfica anterior.
, es decir, cuando g vale 0, tal como quedó reflejada en una gráfica anterior.
Para deducir la fórmula que nos va a permitir calcular la altura máxima alcanzada por un móvil en su movimiento parabólico completo nos remontamos a  (velocidad final es igual a la inicial más la aceleración por el tiempo).
(velocidad final es igual a la inicial más la aceleración por el tiempo).
En nuestro caso actual:
Como Vy vale 0, nos queda: 
Vemos que 
Despejamos 
Sabemos que  y lo sustituimos en la igualdad anterior:
y lo sustituimos en la igualdad anterior:

Sirviéndonos de  y adecuando a lo que estamos estudiando en este momento podemos escribir llamando:
y adecuando a lo que estamos estudiando en este momento podemos escribir llamando:  a la altura máxima
a la altura máxima  .
.
Conocemos el valor del  que lo sustituimos en la igualdad anterior:
que lo sustituimos en la igualdad anterior:

Sustituimos  por su valor
por su valor  elevamos al cuadrado y simplificamos y haciendo paso a paso lo indicado llegamos a:
elevamos al cuadrado y simplificamos y haciendo paso a paso lo indicado llegamos a:

Ya sabemos que la altura máxima que alcanza una trayectoria de un movimiento parabólico completo es:

1.125 ¿Te acuerdas que el señor Pedro Picapiedra sacudía a la pelota de golf a 200 m/s con un ángulo de 30º?
Calcula el punto más alto de la trayectoria.
Respuesta: 510,20 m
Aplicamos la fórmula:

PRÁCTICA: TRAYECTORIA PARABÓLICA INCOMPLETA
Cuando el móvil comienza su movimiento parabólico a una altura distinta de 0 es importante que al factor tiempo lo tengas muy en cuenta.
En el caso de:
A) Tiempo en el que el móvil permanece en movimiento
Debes tener en cuenta de que el movimiento comienza a una determinada altura por lo que y tendrá un determinado valor:

Como el movimiento componente en la dirección vertical y es uniformemente acelerado nos serviremos para su cálculo de la fórmula:

Pero hemos de tener en cuenta de que ahora tenemos un valor inicial de y.
Ahora no partimos del suelo sino de una altura que la representamos por  y lo reflejamos modificando la fórmula anterior:
y lo reflejamos modificando la fórmula anterior:

De esta fórmula nos serviremos para calcular t, quizá el dato que tendremos que utilizar en la resolución de muchos problemas.
1.126 Bartolomé (Bart) Simpson como casi siempre tiene y ejecuta ideas limítrofes con la inocencia, la bondad infinita y otras beatíficas e ingenuas intenciones y acciones.
Esta vez, para una mayor diversión de sus amigos sacude el balón hacia fuera de la isla.
Lo que nos importa es que el balón sale desde una altura de 80 metros con una velocidad de 12 m/s y el ángulo de inclinación es de 45º.
Esto sucede un día de calma chicha (no hay viento) ¿cuánto tiempo tardará el balón en mojarse?

Respuesta: 4,93 s
Solución.
Conocemos el valor de Vo y calculamos el valor de su componente vertical  .
.
Aplicamos la fórmula, sustituimos y hacemos operaciones:

Cuando el balón, “de modo fortuito” llega al agua, el valor de la ordenada y vale 0, pero partió de una altura de 80 m.
No tienes más que aplicar la fórmula anterior:

teniendo en cuenta que el balón salió desde 80 m de altura por lo que añadiremos este valor a la fórmula anterior quedándonos la siguiente ecuación de 2º grado:

Resolviéndola obtenemos:

Tenemos solamente en cuenta el signo positivo, no hay tiempos negativos.
B) Distancia horizontal recorrida por el móvil o alcance
Ahora nos interesa calcular el valor que toma el eje de abscisas que es tan simple como: “espacio es igual a velocidad por el tiempo”. No olvides que se trata de una velocidad constante.
Tenemos que 
Calculamos con anterioridad 
Lo sustituimos en la igualdad anterior  y obtenemos el valor que buscábamos.
y obtenemos el valor que buscábamos.

distancia de la base de esta pared vertical toma “contacto” con el suelo?
Respuesta: 412,85 m
Solución.
Para aplicar la fórmula que acabamos de deducir: 
necesitamos saber el valor de t.
Para ello recurrimos a 
Hallamos el valor de  :
:

Aplicamos este valor en:

Nos queda la ecuación de 2º grado:

Resolviéndola:

Ahora que conocemos el valor de t lo aplicamos en y contestamos a lo que nos han pedido:
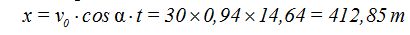
Nota: El valor del coseno lo he obtenido de la tabla de los senos porque al ser complementarios los ángulos, el seno de 30º vale lo mismo que el coseno de 60º (30º+60º=90º), lo mismo que el seno de 70º vale lo mismo que el coseno de 20º (70º+20º=90º). En la siguiente figura, dentro del primer cuadrante compruebas gráficamente lo que acabas de leer: sen 20º = cos 70º:

C) Altura máxima alcanzada en su trayectoria.
El punto de máxima altura que un móvil alcanza en su trayectoria parabólica es donde su velocidad de dirección vertical es  .
.
No importa que la trayectoria parabólica sea completa o no.
Su fórmula sabemos que es: 
De esta fórmula despejas t para después sustituirla en la fórmula de la altura máxima estudiada en este mismo apartado C) al referirnos al movimiento parabólico completo.
En este caso debes tener en cuenta que hay un punto de partida a una altura Yo y a la fórmula de la altura máxima alcanzada hemos de tenerla en cuenta por lo que la fórmula se nos convierte en:

No tenemos más que sustituir el valor de t.
1.128 Recordarás que el señor Picapiedra lanzaba la pelota de golf a 200 m/s con ángulo de 30º.

Ahora, el golpe lo da a 100 m del suelo.
¿Cuál es la altura máxima que alcanza la pelota en su trayectoria parabólica?
Respuesta: 610,2 m
Solución.
Sabemos que D. Pedro sacude a la pelota con una velocidad inicial de 200 m/s, es decir, que el vector velocidad inicial  equivale a la resultante de
equivale a la resultante de  y
y  y de éstas necesito conocer su magnitud o módulo.
y de éstas necesito conocer su magnitud o módulo.
Sabemos que 
Cuando la pelota de golf llega al punto más alto, la velocidad ascendente es cero 
Lo que significa que 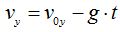 y sustituyo los valores que conozco:
y sustituyo los valores que conozco:  .
.
Ahora recurro, una vez más, a la fórmula:

Sustituyendo valores conocidos:

