Exigencias del movimiento compuesto
A medida que vas leyendo lo relativo al movimiento compuesto da la impresión que hay algunas cosas de entremezclarse y esto nos exige, como siempre, tener muy claras las ideas.
Lo primero que necesitas conocer bien es el tipo de cada uno de los movimientos simples que forman el movimiento compuesto para de esta forma aplicar sus propias ecuaciones y obtener el resultado correcto.
Esto nos exige también conocer:
a) La posición del móvil.
Es muy sencillo, te basta con sumar vectorialmente los valores de los vectores de posición de los movimientos componentes.
Recordarás que los vectores unitarios son vectores cuyo módulo vale 1.
En este caso y en lo que se refiere al plano, tienes dos módulos unitarios: el relativo al eje x que lo representamos por 
y al eje y que lo representamos por 
.
En un eje de coordenadas a los vectores unitarios los representamos:
Para que el módulo valga 1, uno de sus componentes valdrá 0.
El módulo del vector 
tiene por componentes (1,0) y el vector unitario 
tiene por componentes (0,1).
En ambos casos la resultante vale:
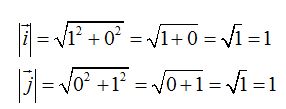
Según lo que acabamos de decir podremos escribir que la posición de la barca en un punto cualquiera del río la podemos señalar con 
por ejemplo, siendo x=7 e y=5 la resultante r nos viene dada por:
Para conocer la medida, el tamaño, el módulo de 
tendremos que calcular:
Gráficamente lo tienes indicado en la figura siguiente:
b) Como estamos tratando la composición de movimientos hemos de referirnos a las velocidades de cada uno de los movimientos simples sin olvidarnos que son magnitudes vectoriales.
En el ejemplo de la barca, la velocidad resultante ves que tiene dos componentes, lo compruebas en la figura siguiente que son 
y 
:
¿Cómo calculas la velocidad resultante de la barca?
Sencillamente sumando vectorialmente las velocidades de sus componentes.
¿Cuáles son las componentes del vector velocidad?
En primer lugar, si te dan la velocidad de la corriente puedes representarla con Vx y la velocidad que consigues con los remos con Vy.
En segundo lugar, dirás con razón que no son valores vectoriales y los necesitamos como vectoriales para hallar la velocidad real 
de la barca.
A la velocidad 
(magnitud escalar) la transformas en vectorial multiplicando por 
y a 
por 
y de este modo llegamos a:
Para calcular la velocidad resultante no tienes más que calcular el módulo de 
que por Pitágoras y sabiendo que 
vale 1 lo mismo que 
llegamos a:
c) Otro dato que necesitamos conocer es la trayectoria recorrida por el móvil.
Este dato lo obtenemos fácilmente del modo siguiente:
Imagina que te dicen:
Representa gráficamente la trayectoria de la barca transcurridos t segundos sabiendo que su velocidad por segundo es de Vx metros sin utilizar los remos:
Considerando el punto amarillo como partida de la barca impulsada por la corriente del río, el valor de x depende de la velocidad de la corriente y del tiempo lo que nos permite escribir:
La misma consideración podemos hacer ahora teniendo en cuenta la velocidad que impulsamos con los remos sin tener en cuenta la corriente del río:
El valor de y depende del impulso que producimos con los remos y del tiempo que estemos remando por lo que escribiremos:
La composición de estos dos movimientos bajo el punto de vista gráfico es:
Vemos que la tangente del ángulo α nos vendrá dada por:
1.119 Tenemos un río cuya anchura en el lugar que queremos cruzarlo es de 100 m.
La velocidad de la corriente es de 3 m/s.
Con los remos conseguimos 2 m/s siempre perpendicular a la corriente.
Deseamos saber:
1) La velocidad de la barca respecto a la orilla de la que partió.
2) El tiempo que tardamos en llegar a la otra orilla.
3) Los metros que hemos recorrido dentro de ella.
Respuestas: 1ª) 3,6 m/s; 2ª) 50 s; 3ª) 180,28 m
Solución.
1) Sabemos por las fórmulas deducidas que 
.
No tienes más que sustituir por los datos que conocemos y obtenemos:
Calculamos el módulo del vector velocidad:
2) Conocemos la anchura del río que son 100 m y la velocidad que producimos con los remos, 2 m/s.
Como las velocidades actúan independientemente tendremos que el tiempo en cruzar el río será:
3) Vamos a calcular las coordenadas de posición para conocer el desplazamiento que hemos hecho dentro de la barca.
El valor de abscisa nos vendrá dado por:
El valor de ordenada procede de:
Aplicando la fórmula obtenida con anterioridad en la que
1.120 Una avioneta vuela a 80 m. de altura sobre el mar con una velocidad de 360 Km/h y el piloto trata de que el náufrago de isla tenga algo que comer hasta que vengan por mar a rescatarlo.
¿A qué distancia de la isla dejará caer el paquete para que el isleño no tenga problemas en hacerse con la comida?
Se supone que apenas hay viento.
Respuesta: 400 m
Solución.
Vamos a animar la resolución dibujando la situación:
En primer lugar tenemos que ver que el paquete “vuela” a 360 Km/h (porque sale de la avioneta) cuya velocidad la pasamos a metros por segundo:
En segundo lugar recordamos que tenemos, por un lado, la distancia que debe recorrer el paquete independientemente del movimiento de la caída libre de dicho paquete por causa de la atracción de la tierra que la suponemos g=10m/s2.
Sabemos que en la caída de los cuerpos la altura depende de la atracción de la tierra (g) y del tiempo que esté cayendo el objeto aplicando:
calculamos el tiempo:
El paquete tarda en caer 4 segundos, es decir, el paquete está en movimiento rectilíneo durante este tiempo.
Conocemos la fórmula del espacio que es: e = v . t sustituyendo valores que conocemos, velocidad del paquete 100 m/s y el tiempo que dura el movimiento que son 4 s:
1.121 ¿Cómo ve el piloto de la avioneta en 5 momentos la caída del paquete?
Respuesta: Caída vertical.
Solución
Como el paquete y la avioneta vuelan a la misma velocidad (teniendo en cuenta nulo el rozamiento del aire) siempre la verá en su vertical pero con un tamaño más pequeño porque la atracción de la tierra produce el movimiento descendente:
1.122 Antes de responder piensa bien lo que vas a decir. Imagina que la corriente de un río aumenta.
Se pregunta, razonando la respuesta, el mismo nadador ¿tardará más tiempo en cruzarlo de cuando tenía menor corriente?
Respuesta: Como los movimientos (corriente del río y la que produce con la velocidad que obtiene nadando), son independientes y la anchura del río no ha variado tardará el mismo tiempo.
No olvides que cada uno de los movimientos simples actúa por su cuenta, por separado.
