Resultante de la suma de dos vectores
Habrás estudiado en matemáticas a calcular la suma de vectores.
Utilizando el método del paralelogramo tienes a continuación la suma gráfica de dos vectores:
Tenemos que sumar los vectores 
y 
:
A partir del extremo del vector 
trazamos una paralela del vector 
y hacemos lo mismo trazando una paralela del vector 
a partir del final del vector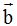 
(las paralelas las tienes en color rojo):
La suma de los 
Hemos creado un paralelogramo y la diagonal que une el origen de los dos vectores con el punto de concurrencia de sus paralelas equivale a la suma.
Los vectores 
y 
son las componentes del vector 
.
COMPONENTES DE LA ACELERACIÓN EN EL MOVIMIENTO CIRCULAR.
Algo parecido nos sucede con las aceleraciones tangencial y normal en cualquier trayectoria circular o curvilínea.
Estas dos aceleraciones son perpendiculares entre sí. Sabemos que la primera mide el cambio de la rapidez y la segunda mide el cambio que se experimenta en la dirección del movimiento.
Hemos tomado tres puntos (en rojo) de la trayectoria (en amarillo) fijando en ellos las aceleraciones tangenciales y normales que como ves, son las componentes del vector de la aceleración instantánea 
.
La aceleración de un móvil que se desplaza por una trayectoria curvilínea como en este caso, se ve afectada por sus dos componentes y podemos escribir:
El módulo del vector aceleración instantánea fijándonos en cualquiera de los triángulos rectángulos formados en cada punto de la trayectoria curvilínea lo obtenemos por Pitágoras:
1.117 Un móvil en su movimiento circular uniformemente acelerado, describe una circunferencia de 30 cm de radio.
Cuando pasa por el punto P1 su rapidez es de 12 cm/s y cuando pasa por P2, 0,1 segundo después, su rapidez es de 14 cm/s.
Calcula:
- la aceleración total a, a su paso por P1 y
- el ángulo φ que formará con el radio.
Respuestas: 1ª) 20,57 cm/s2; 2ª 72,5º
Solución.
Es buena costumbre resolver los problemas que te proponen, siempre que se pueda, acompañándote de sencillos dibujos.
Después de leer el texto del problema podríamos realizar la figura siguiente:
Para conocer la aceleración total necesitamos conocer la aceleración tangencial y la aceleración normal.
Calculamos la aceleración tangencial en el punto P1 sin tener en cuenta la dirección del móvil:
La aceleración normal en el punto anterior es teniendo en cuenta su dirección:
El módulo de la aceleración total vale 
.
Sustituyendo los valores que conocemos tenemos:
Para calcular el ángulo que forma la aceleración instantánea a, tomamos de la última figura la zona que nos interesa y la giramos para ver con más claridad el valor de la tangente de φ:
Vemos que la
Pasamos a grados calculando el arco cuya tangente vale 4,1667 con una calculadora y si no con cualquier conversor on line que dispones en Internet:
1.118 Un volante de inercia que parte del reposo al cabo de 1,2 segundos el vector de su aceleración instantánea a forma con el vector que representa a la aceleración tangencial at un ángulo de 33º. Calcula su aceleración angular α.
Respuesta:
Solución.
En primer lugar realizamos la figura:
Analizando la figura vemos que:
Sabemos que derivando la velocidad lineal cuando Δt tiende a cero obtenemos la aceleración tangencial, es decir, 
y haciendo operaciones en la última igualdad llegamos a:
Ten en cuenta que at se refiere a la aceleración tangencial y dt se refiere a la diferencial del tiempo por lo que no tienen nada en común.
Integramos ambos miembros de la igualdad teniendo en cuenta el tiempo en que el movimiento ha durado, se ha iniciado en 0 segundos y ha finalizado al cabo de 1,2 segundos:
En el primer miembro la integral y la derivada “se simplifican” y nos queda v.
En el segundo miembro at es una constante a la hora de integrar pues la diferencial se refiere al tiempo (dt) , la t de at se refiere a la aceleración tangencial por lo que la sacamos fuera de la integral y escribimos:
Resolvemos esta integral y obtenemos:
Hemos quedado al principio con la igualdad:
La tangente de 33º vale 0,65, luego:
Dedujimos el valor de 
y hemos calculado el valor 
sustituyéndolo en esta fórmula: 
Este valor de an lo reemplazamos en y simplificamos (I):
Sabemos que 
y lo sustituimos y simplificamos en (II):
Despejamos α:
