Velocidad lineal o tangencial

Existe un juego interesante para practicarlo entre 4 o 5 amigos en la playa o un campo de fútbol, etc. Consiste en tomarse las manos y como si fuese un tren, el primero comienza a correr y cuando todos están en plena carrera da un giro rápido y veréis las dificultades del último de la cadena para seguir el ritmo de los demás.

Si en lugar de 4 o 5 fuesen 7 u 8 personas, al último le es imposible seguir asido después que el primero haya girado en su carrera.

En la figura imaginamos 5 personas corriendo tomadas de la mano. Si el primero gira a una velocidad moderada, al quinto corredor le resultará mantener la velocidad tangencial que ha adquirido.

Cuanto mayor velocidad angular imprima el primero (ω) o cuanto más personas intervienen (Radio) la velocidad (v) del último de la cadena se hace mayor.

RELACIÓN ENTRE VELOCIDAD ANGULAR Y LINEAL O TANGENCIAL.

La velocidad de cualquier partícula situada sobre la línea de la circunferencia podemos escribirla:

Podemos transformar la igualdad anterior según lo estudiado anteriormente en: 

Ambas velocidades se relacionan con el radio.

1.90 Observa bien la siguiente figura:

Se trata de dos poleas: ruedas con un canal por su circunferencia por donde pasan correas o cadenas que se utilizan para la transmisión de movimientos como tienes en la foto siguiente:

La de menor diámetro suponemos que está unida al eje de un motor eléctrico y gracias a la correa de transmisión (línea amarilla) hace girar a la polea de mayor diámetro.

Una vez en marcha el motor ¿cuál de las dos poleas tiene mayor velocidad lineal y por qué?

Respuesta: La misma porque ambos discos llevan la velocidad de la correa.

1.91 Continuamos con los datos del problema anterior y se pregunta ¿cuál de las poleas lleva mayor velocidad angular, y si hay diferencia, cuánto vale ésta?

Respuesta: La polea de menor radio lleva doble velocidad angular que la polea de mayor radio.

Solución.

Podemos resolver de varios modos, tienes a continuación uno de ellos partiendo de que sus velocidades lineales son iguales:

Si a  le das un valor cualquiera, en este caso depende de las r.p.m. del motor, comprobarás que  adquiere una velocidad doble.

1.92 Las dos poleas de la figura siguiente están comunicadas por una correa. Conocemos sus radios y sabemos que la de mayor diámetro gira a 15 revoluciones por cada 3 segundos y queremos saber la frecuencia de la polea de menor radio:

Respuesta: 9 r.p.s.

Solución.

La frecuencia de la polea mayor es: 

Si la frecuencia de la menor es:   podemos escribir la siguiente igualdad: 

Sustituyendo por sus valores conocidos tenemos:

1.93 En la figura siguiente puedes ver el plato y el piñón de una bicicleta. Más o menos dos poleas comunicadas por una cadena:

Imagina que vas montado en esta bicicleta y que el piñón tiene un radio de 6 cm. y el plato 10 cm.

Vas pedaleando (plato) por un terreno llano a la misma frecuencia de 40 r.p.m.

Responde a las siguientes preguntas:

1. ¿Cuál es la frecuencia del piñón?
2. ¿Cuáles son las velocidades angulares de cada una?
3. ¿Qué diente lleva más velocidad, el del piñón o el de la cadena?
4. ¿Cuáles son las velocidades lineales del piñón y la cadena?

Razona las respuestas.

Respuestas: 1ª.- 1,11 r.p.s. 2ª.- 6,97 rad/s el piñón y 4,19 rad/s el plato, 3ª.- Iguales, 4ª.- 6,67 m/s.

Solución.

1) Sabemos que:

de donde deducimos que:

es decir, que las frecuencias son inversamente proporcionales a los radios.

La frecuencia del plato por segundo: 

Despejamos en (I) la frecuencia del piñón:

2) Las velocidades angulares en radianes por segundo son:

3) Un diente del piñón, un diente del plato y la cadena llevan la velocidad de ésta.

4) La última respuesta nos sirve de comprobación:

La velocidad lineal nos viene dada por: 

Sustituyendo valores obtenemos: 

Vemos que las velocidades lineales son iguales.

1.94 ¿Se puede afirmar: “dos poleas de distinto diámetro, a mayor radio, mayor es su velocidad angular”?

Razona tu respuesta.

Respuesta: No se puede afirmar porque es FALSO.

Solución.

Supongamos que la polea 1ª tiene un radio    y lleva una velocidad angular .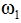

La segunda polea tiene un radio que mide  y lleva una velocidad de.

Suponemos unidas ambas poleas por una correa que implica que ambas llevan la misma velocidad lineal por lo que podemos escribir: (ambos productos son iguales).

Podemos deducir que si   aumenta,   tendrá que valer menos para que la igualdad permanezca, o viceversa.

Suceden las mismas consideraciones para la otra polea.

Llegamos a: a mayor radio, menor velocidad angular y viceversa.