Asociación de pilas en serie y en paralelo

También a las pilas podemos asociarlas en serie o en paralelo.

Conexión de pilas en serie:

Basta ponerlas una detrás de otra. Positivo de una con negativo de la siguiente.

De este modo conseguimos sumar sus diferencias de potencial:

La Intensidad se mantiene igual: 

En teoría podemos conectarlas como acabas de leer, con potenciales e intensidades diferentes.

Con la Intensidad sucede parecido a lo pasa en un equipo de fútbol, baloncesto, cualquier deporte que se juegue de modo colectivo. Si hay un jugador que es un gran mago del balón pero es lento, no cuentes con él, si eres entrenador, porque el equipo correrá a la velocidad del más lento.

Si tienes una pila de 0,4A y otra de 1A, colocadas en serie la Intensidad será 0,4A.

En la práctica es mejor tener en cuenta unos sencillos consejos:

1.- Cuando coloques pilas en serie o paralelo procura que sean de la misma marca.

2.- No conectes usadas con pilas a estrenar.

No pierdas de vista que cuando sumamos los voltajes, también sumamos sus resistencias internas y provocamos con ello una pérdida de energía.

7.29 Al conectar en serie hemos dicho que las intensidades son iguales.

Tenemos 3 pilas en serie:

Intensidad de la 1ª pila 0,5A, la 2ª de 0,3A y la 3ª de 0,1 A

¿Cuál es la Intensidad de esta asociación?

Respuesta: 0,1A

Solución

La respuesta ha quedado indicada en la explicación previa.

Conexión de pilas en paralelo:

Hacemos que un conductor esté conectado a los electrodos positivos y otro a los negativos.

Entre estos dos conductores se establece una corriente eléctrica en la que su diferencia de potencial es la de cada una cuidando que todas han de tener la misma y su Intensidad al poderse reunir en un punto (nodo) es la suma de todas.

7.30 En el circuito que tienes a continuación calcula la Intensidad del mismo:

Respuesta: 0,1 amperio

Solución

Cuando tengas dos fuentes de alimentación en serie fíjate si la polaridad de una al prolongarla, coincide con la polaridad del mismo signo de la siguiente se restan las diferencias de potencial.

Esto significa que en el circuito tenemos 20V – 10V = 10V Como conocemos la Resistencia, aplicamos la ley de Ohm:

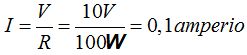
7.31 En la figura siguiente tienes dos pilas iguales en cuanto a fuerza electromotriz (ε) 3V cada una y resistencia interna 0,5 ohmios cada una también.

Calcula la Intensidad de la corriente que atraviesa la Resistencia externa de 10 ohmios.

Respuesta: 0,54A

Solución

Al estar en serie los generadores sumamos sus fuerzas electromotrices obteniendo un total de 3V + 3V = 6V.

Las tres Resistencias (2 internas y una externa) están en serie por lo que su equivalente es: 0,5Ω + 0,5Ω + 10 = 11ohmios.

Aplicando la ley de Ohm: 

7.32 En este problema calculamos lo mismo que en el anterior pero ahora consideramos que las fuentes de alimentación están en paralelo:

Respuesta: 0,29A

Solución

Ahora las resistencias internas se hallan en paralelo siendo su equivalente:

La diferencia de potencial al estar las fuentes en paralelo no varía por lo que aplicando la ley de Ohm y sabiendo que la resistencia interna equivalente está en serie con la Resistencia externa de 10 ohmios:

7.33 En el circuito:

Calcula la Intensidad de la corriente que circula.

Respuesta: 0,1A

Solución

Sabemos por las leyes de Kirchoff que la suma de todas las diferencias de potencial en un circuito es cero.

Elegimos el sentido (flecha curva azul) de la corriente en el circuito que la representamos con I₁ y nos situamos en el punto de partida P:

Siguiendo el sentido prefijado y saliendo de P analizamos las diferencias de potencial positivas y negativas que encontramos.

Estas diferencias de potencial pueden ser positivas o negativas. Tomamos como positivas las la diferencia de potencial que van de + a – (subida de tensión), y como negativas, las que al pasar por una Resistencia se produce una caída de tensión, pasando de – a +.

Para facilitar nuestro análisis añadimos en el esquema del circuito los signos apropiados:

La fuente de alimentación ya indica su polaridad.

Al salir de P en el sentido indicado nos encontramos con una diferencia de potencial de 3V que va de – a +, por lo tanto, la consideramos positiva, seguidamente tenemos una Resistencia de 20 ohmios indicándonos que la corriente va de + a – cuyo valor es negativo y su magnitud aplicando la ley de Ohm: V = R . I tendremos una caída de potencial de 20I₁ con signo negativo.

Nos sucede lo mismo con la siguiente Resistencia de 10 ohmios que produce una nueva caída de tensión de V = 10I₁ con signo negativo también.

7.34 Añadimos una malla al circuito anterior incorporando otra pila y una nueva Resistencia y suponemos que las resistencias internas son muy pequeñas por lo que no las tenemos en cuenta:

¿Cuánto vale la Intensidad de la corriente en cada Resistencia?

Respuestas:

Solución

En este caso tenemos que hallar la Intensidad de la corriente en cada Resistencia y no en la malla.

Esto supone que por cada Resistencia pasa una Intensidad resultante de las que recibe de ambas fuentes de alimentación.

Teniendo en cuenta lo que acabas de leer suponemos que por la Resistencia de 20 ohmios pasa una intensidad I₁, por la de 10 ohmios la Intensidad es I₂ y por la de 30 ohmios es de I₃ amperios:

Debes tener en cuenta que necesitas 3 ecuaciones debido a que has de deducir el valor de 3 incógnitas, es decir, 3 Intensidades diferentes.

Para la 1ª ecuación y tomando como referencia el nodo A hacemos uso de la 1ª ley de Kirchoff y se cumplirá: I₁ = I₂ +I₃ o lo que es lo mismo, cantidad de corriente que entra es igual a la que sale.

Para la 2ª ecuación aplicamos la 2ª ley de Kirchoff y para no complicarnos mucho tomamos como referencia la malla de la figura:

Recuerda que en una malla la suma de todas las caídas de tensión ha de ser igual a la suministrada por la pila.

Si te parece más cómoda la forma de recordar puedes utilizar: en una malla la suma (algebraica) de todas las tensiones es cero.

Fijamos el sentido de la corriente en el sentido indicado por la flecha curva de color azul.

Se ha de cumplir que la fuerza electromotriz de la pila ε es 3V y las caídas de tensión producidas por las Resistencias de 20 y 10 ohmios son: I₁ . 20 y I₂ . 10 respectivamente.

Como en ambos casos el sentido de las corrientes es el que previamente hemos fijado, no hay cambio de signo.

Se cumplirá: 3V = I₁.20 + I₂.10

Para la 3ª ecuación consideramos la malla que tenemos en la siguiente figura sabiendo que una trayectoria o camino cerrado es una malla:

Partiendo del punto B y siguiendo las caídas de tensión nos encontramos con 3V que al ir de menos a más tendrá signo positivo, seguidamente nos encontramos con Resistencia de 20 ohmios que como produce una caída de tensión irá de más a menos por lo que el resultado: 20 . I₁ tiene signo negativo.

Continuamos nuestro camino y ahora estamos ante una Resistencia de 30 ohmios con la Intensidad que hemos supuesto de I₃. La corriente sigue el mismo sentido que en el caso anterior y tendremos una caída de potencial igual a 30 . I₃ con signo también negativo.

Por fin nos encontramos con el positivo de una pila de 3V cuya corriente va de + a – donde se produce una caída de potencial de

Terminado nuestro recorrido llegamos a la siguiente ecuación:

3 – 20.I₁ – 30.I₃ – 9 = 0

Las tres ecuaciones (texto de color rojo) son las que nos van a permitir deducir los valores de cada una de las Intensidades.

El sistema de estas tres ecuaciones es:

Sustituimos I₁   por   en la 2ª y 3ª ecuaciones:

Quitamos paréntesis y reducimos los términos semejantes:

Utilizamos el método de igualación. Igualamos los valores de I₂:

El valor de I₁ nos viene dado por la suma de las dos intensidades anteriores: