Superposición de fuerzas electrostáticas
Hasta ahora hemos supuesto dos cargas q1 y q2 tratando de comprender la Fuerza (atractiva o repulsiva) que una ejerce sobre otra.
Lo normal no es que estén presentes justamente dos cargas eléctricas, seguro que habrá más de dos.
Las Fuerzas son muy independientes, cada una actúa sin tener en cuenta la existencia de otras.
Vamos a suponer la existencia de las tres cargas siguientes:

Queremos saber cuál es la Fuerza total que actúa en la carga q1 por la acción de las cargas q2 y q3.
En primer lugar trazo las líneas de acción de cada fuerza:

La Fuerza que realiza q2 sobre q1  veo que es repulsiva porque las cargas tienen el mismo signo:
veo que es repulsiva porque las cargas tienen el mismo signo:

La Fuerza que q3 ejerce sobre q1 es atractiva por tener cargas eléctricas de signos contrarios y lo represento del modo siguiente:

Veo que hay dos Fuerzas,  actuando sobre q1.
actuando sobre q1.
Pero, ¿cuánto vale la suma de ambas Fuerzas?
No se trata de una suma de valores escalares (4kg +2kg = 6kg), se trata de magnitudes vectoriales.
Un modo gráfico de calcular la suma sería aplicando la ley del paralelogramo (estudiado en Matemáticas).
A partir del vector 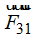 dibujo una paralela que corresponda al vector
dibujo una paralela que corresponda al vector 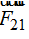 :
:

y otra recta paralela a partir del vector 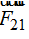 al vector
al vector 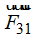

Gráficamente la suma de ambos vectores será la resultante: 

Lo mismo podríamos hacer con más cargas eléctricas:
Supongamos las cargas q1, q2, q3, q4 …. y otra carga q0 y queremos saber la Fuerza resultante o si quieres, la Fuerza total que actúa sobre q0 por causa del resto de las cargas suponiendo iguales sus signos y medidas de las cargas.
Gráficamente lo representamos:

Las Fuerzas son repulsivas por tener signos iguales. Cada una actúa sobre su línea de dirección de la Fuerza.
La carga q0 recibe por causa de q1 una Fuerza de repulsión de  lo mismo que por la carga q2 una Fuerza
lo mismo que por la carga q2 una Fuerza  , por la q3 una Fuerza
, por la q3 una Fuerza  y por la carga q4 una Fuerza
y por la carga q4 una Fuerza  .
.
Llamando  al vector de la Fuerza correspondiente a la suma de todas las Fuerzas que ha registrado la carga q0 ¿Cómo calculamos la suma de todas las Fuerzas repulsivas, es decir:
al vector de la Fuerza correspondiente a la suma de todas las Fuerzas que ha registrado la carga q0 ¿Cómo calculamos la suma de todas las Fuerzas repulsivas, es decir:
 ?
?
Recuerda que estamos manejando vectores.
El modo más elemental es la de utilizar la ley del paralelogramo:
Primero tomamos los dos primeros sumandos sin olvidarnos que son vectores:

Es decir sumamos  :
:

y hemos obtenido una resultante en color azul.
Ahora sumamos los vectores: 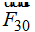 +
+ 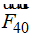 y calculamos la resultante también en color azul:
y calculamos la resultante también en color azul:

Hallamos la resultante 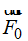 tomando como sumandos los dos vectores con color azul y así determinamos la suma total, utilizando la ley del paralelogramo:
tomando como sumandos los dos vectores con color azul y así determinamos la suma total, utilizando la ley del paralelogramo:

Según lo que estás estudiando cabe preguntarse:
¿En qué consiste el principio de superposición de Fuerzas?
Si tenemos una carga determinada dentro de un campo eléctrico formado por varias cargas, la suma de las Fuerzas de cada una de éstas equivale a la Fuerza total que experimenta aquélla. Lo que equivale a decir que el campo eléctrico que se crea en un punto por la existencia de cargas eléctricas equivale a la suma vectorial de las Fuerzas que cada carga crea en ese punto.
El paso siguiente es el de calcular la magnitud, dirección y sentido de la resultante y para ello vamos a resolver el problema siguiente:
En los vértices de un triángulo equilátero se encuentran situadas las cargas siguientes:

Queremos conocer los datos de la Fuerza resultante en la carga (A) creadas por las Fuerzas de las cargas (B) y (C).
Respuesta:
-54mNî
Solución:
Las cargas (B) y (A) tienen signos diferentes lo que significa que se atraen. Representamos con el vector  a la Fuerza creada en (A) por causa de la carga (B):
a la Fuerza creada en (A) por causa de la carga (B):

Para hallar la resultante sumamos los vectores 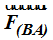 y
y  utilizando la ley del paralelogramo, llamando
utilizando la ley del paralelogramo, llamando  a la resultante:
a la resultante:

Este vector tiene una medida, tiene una dirección y un sentido pero ¿cómo medirlo? con referencia ¿a qué hacemos los cálculos?
Una cosa muy sencilla es la de situar un eje de coordenadas en el punto más conveniente para lograr los resultados que pretendemos y lo hacemos tal como lo tienes en la figura siguiente:

Vamos a deducir las componentes de los vectores de cada uno de estos dos sumandos para lo que echamos mano de lo estudiado en Trigonometría.
Observa con atención a las componentes del vector 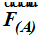 que como sabes son
que como sabes son 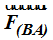 y
y 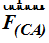 . De estos dos vectores podemos conocer, por los datos del problema, su módulo, medida o tamaño para el vector
. De estos dos vectores podemos conocer, por los datos del problema, su módulo, medida o tamaño para el vector
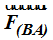 y aplicando la ley Coulomb y sustituir valores conocidos:
y aplicando la ley Coulomb y sustituir valores conocidos:

Ten cuidado, se trata del valor, magnitud o tamaño de la Fuerza (no lleva la flecha sobre la F, luego ya no es un vector sino un número) que la partícula en (B) ejerce sobre la carga en (A) sin importarnos el signo del valor que para eso lo indicaremos con su vector unitario correspondiente.
Continuamos haciendo operaciones:

Realizamos el mismo cálculo para saber la Fuerza que la carga en (C) ejerce sobre la que se halla en (A). Ambas tienen cargas del mismo signo lo que hace que se repelan creando la fuerza 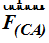 :
:


Los resultados son iguales debido a que las cargas y distancias tienen los mismos valores absolutos.
Ahora conocemos los módulos de los vectores 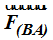 y
y 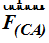 que son
que son 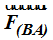 = 0,054N y
= 0,054N y
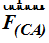 = 0,054N:
= 0,054N:

Fíjate que las Fuerzas al estar sin la flecha sobre ellas que las identifica como vector significan el valor de su módulo.
Sabemos por lo estudiado en Trigonometría que el seno y coseno de un ángulo son iguales a:

¿Cómo indico en el eje de coordenadas la posición de estos valores?
Para este cometido dispongo de los vectores unitarios  (eje de las x) y
(eje de las x) y  (eje de las y). Estos datos los situamos en la figura siguiente:
(eje de las y). Estos datos los situamos en la figura siguiente:

¿Por qué el ángulo indicado es de 60º?
Sabemos de haberlo estudiado en Geometría que dos rectas paralelas cortadas por otra se forman 8 ángulos, 4 internos (amarillo) iguales dos a dos y 4 externos (azul) iguales dos a dos:

Tenemos en cuenta los dos internos alternos que nos interesan y los comparamos con el triángulo equilátero en cuyos vértices se hallan las cargas:







El resultado lo damos en milinewtons para evitar decimales, pero no pasa nada si el resultado los expresas en N.
