Cálculo del ángulo de refracción
Cuando un rayo de luz pasa de un medio a otro de distinto índice de refracción produce con la normal un determinado ángulo tanto cuando incide (ángulo de incidencia) en otro medio como cuando se refracta (ángulo de refracción), es lo que representamos en la siguiente figura:

Antes de comenzar con la demostración debes conocer el fenómeno siguiente que puedes experimentar en tu casa:

Se trata de un carrito aunque te puede servir un patinete, un coche de juguete, etc.
En un lugar donde haya una pendiente le dejas rodar pero de modo que a partir de un lugar de la pendiente, el suelo no esté bien pulimentado o si quieres, echas arena, lo pones rugoso raspando el suelo, etc.
Notarás que el carrito al llegar a un suelo en peores condiciones para rodar gira hacia la normal, es que como cuando el rayo de luz se refracta, tiende a acortar el camino.
Realizado en plan casero y de un modo muy rudimentario tienes las fotografías siguientes que no te costará mejorarlas:

1.- El camión grúa (de juguete) preparado para deslizarse por la pendiente de madera fina.
2.- Entra en una franja cuyo suelo es más refringente que la fina madera (jabón en polvo).
3.- Huella que dejan las ruedas: al entrar en el suelo del jabón en polvo se aproxima a la normal y cuando sale de este suelo y entrar en otro menos refringente se aleja de la normal.
Esto te puede dar la impresión que no tiene mucha importancia, pero no es así.
Fíjate bien en lo que vas a estudiar a continuación:

Hemos representado de un modo muy elemental el camión de juguete.
Se desliza sobre un suelo de madera poco refringente.
La rueda delantera A del camión llega al suelo más refringente (polvo de jabón).
Se nos ha quedado determinado el triángulo ABC:

Ahora tenemos el momento en el que la rueda A que avanza por camino refractado se halla en el punto D y la rueda B llega al suelo más refringente:

Suponiendo que la velocidad del camión sobre suelo de polvo de jabón es de v2 m/sel espacio recorrido por la rueda A en t segundos ha sido, es decir, la distancia AD vale:

Verás que la delantera del camión llegaba con un ángulo de incidencia i.
Los ángulos de incidencia que se forman son varios, iguales, por supuesto, formados por lados perpendiculares.
Recuerda que hemos dicho que la rueda A ha tardado t segundos en llegar a D sobre el suelo de polvo de jabón, pero en este tiempo ¿qué distancia ha recorrido la otra rueda delantera?
El recorrido que hace es de B a C. Lo puedes observar en la siguiente figura.
Supongamos que la velocidad que el camión lleva por el suelo de madera fina es v1.
Llamando n1 al índice de refracción en este medio podemos escribir:

Lo mismo hacemos en el medio más refringente.
Representamos con v2 a la velocidad en este medio y con n2 al índice de refracción por lo que 

Supongamos ahora que la rueda que se encontraba en B tarda t segundos en llegar a C con velocidad v1, será el mismo tiempo de lo que tarda la rueda que se encontraba en A para llegar a D con velocidad v2.
La distancia BC equivale a: 
La distancia AD es de: 
Dividimos estas dos igualdades y simplificamos:

Fíjate bien en los triángulos rectángulos: ABC y ADC
Haciendo uso de lo aprendido en Trigonometría tendremos:

Dividimos entre sí a estas dos igualdades simplificando:

Sustituimos a BC y AD por los valores que anteriormente hemos hallado:

Estudiamos que:

Supongamos que el índice de refracción en suelo de madera es n1 y sobre suelo de jabón en polvo n2.
Esto significa que: 
Estas igualdades podemos escribirlas también: 
Dividimos estas dos igualdades entre sí y simplificamos:

Sustituimos estos valores en (I):

Producto de extremos igual al producto de medios:

Fórmula muy útil para resolver problemas en la que te pidan un dato y de un modo u otro, generalmente, te facilitarán los otros tres.
Por si te queda alguna duda respecto a lo que hemos estudiado, me refiero al camión de juguete. Es posible que te preguntes “¿qué tiene que ver la rueda delantera derecha de un camión de juguete, … y luego la rueda izquierda… si lo que estamos estudiando es el rayo de luz su reflexión, incidencia y refracción?”
Cuando nos referimos al rayo de luz no es solamente un casi invisible “hilo” de luz, se trata de un conjunto de rayos, de un haz de rayos que tienen un frente, una delantera y si no lo ves claro observa las fotografías siguientes:

Ves los rayos de sol que entran por la claraboya del tejado, los que penetran por un agujero natural en una cueva marina, y en las otras dos puedes contemplar los haces de luz dentro del agua.
Puedo tomar como ejemplo la delantera de este haz de rayos que cuando penetran en otro medio más refringente se refracta:

5.14 Un rayo de luz incide sobre las aguas tranquilas y transparentes de un lago con un ángulo de 30º.
Sabemos que el índice de refracción de la luz en el aire vale 1 y en el agua 1,33 ¿cuánto vale el ángulo de refracción?
Respuesta: 22,08º
Utilizamos la fórmula anteriormente deducida: 
Los datos que conoces son:

Sustituimos los valores que conocemos en la fórmula:
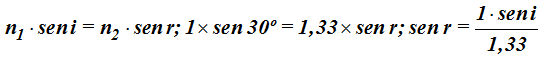
Miramos en las Tablas Trigonométricas el valor del seno de 30º y vemos que corresponde a 0,5 y despejamos el sen r:

Ves que sen r vale 0,37593985 y necesitamos saber cuál es el ángulo del arco cuyo seno mide esta cantidad.
Para calcular a cuantos grados corresponde la longitud de arco anterior con Tablas, Calculadora, Hoja de Cálculo, etc., hallarás el ángulo :

5.15 Un rayo de luz penetra en un líquido con un ángulo de incidencia de 60º y se desvía 39º.
Respuesta: 124.142Km/s

Siendo n1 el índice de refracción en el aire
n2 el índice de refracción en el líquido
Sabemos que 
Vemos que el ángulo de refracción será: 60º - 39º = 21º
Sustituyendo los valores que conocemos:

Despejamos n2 y hacemos las operaciones indicadas:


Sustituyendo valores conocidos:

Respuesta: 
Nos ayudamos de un sencillo dibujo:

Utilizamos la misma fórmula que en casos anteriores:

Hacemos operaciones:

Sabemos que  donde sustituyendo valores llegamos a:
donde sustituyendo valores llegamos a:

5.17 Imagina una vasija con un foco de luz en el fondo. El índice de refracción del líquido que contiene vale 1,5.
El haz de rayos que sale del foco tiene forma de cono cuya base estaría situada en la superficie y tendría forma de circunferencia cuyo radio mide 0,8m.
Respuesta: 0,8944m
Hacemos una figura que nos ayude a comprender mejor lo que nos pide el problema:

Lo primero que hemos de hacer es calcular el ángulo límite porque nos va a permitir conocer de un modo muy sencillo el coseno de este ángulo que va a corresponder a la altura que nos pide el texto del problema.
Observa la figura siguiente y verás que con la ayuda de la Trigonometría resolvemos lo que nos pide el texto del problema.

Calculamos el ángulo límite.
Hacemos uso de la fórmula como en casos anteriores:

Despejamos sen i:

Hallamos el arco cuyo seno vale 0,6666667: 
Conocemos el ángulo límite que es de 41,81º.
Tenemos un triángulo rectángulo del que conocemos un ángulo que vale 41,81º y otro de 90º.

Sabemos por lo aprendido en Trigonometría teniendo en cuenta la figura precedente:

Sustituyendo valores que conocemos mirando en las Tablas Trigonométricas el valor de la tangente de 41,81º vemos que vale 0,8944173 obtenemos:

5.18 El índice de refracción de un material transparente vale 1,8 y cuando un rayo procedente del aire incide con un ángulo de 45º ¿cuánto vale el ángulo de refracción? y ¿cuánto su ángulo límite?
Respuestas: 1ª) 23,13º; 2ª) 33,75º
Aplico como siempre la fórmula: 
Sustituyendo valores conocidos y haciendo operaciones:

Miramos en unas Tablas Trigonométricas el ángulo cuyo arco mide 0,392837101:

Solución a la 2ª pregunta:
Me ayudo de un sencillo dibujo:

El rayo incidente procede del medio más refringente.
Aplico la fórmula de casi siempre que como es lógico haré las modificaciones que me exige el texto:

El ángulo refractado al cambiar de medio toma la dirección cuyo ángulo vale 90º.

5.19 Un rayo de luz procedente del aire incide en un líquido con un ángulo de 45º y se refracta 30º.
Calcula el ángulo de refracción cuando incide con 90º.
Respuesta: 45º
Seguimos utilizando la fórmula: 
Sustituyendo valores en los dos casos que nos propone el texto del problema obtenemos:

Tenemos en cuenta que los índices de refracción en el aire y en el líquido son respectivamente n1 y n2.

Simplificamos, sustituimos valores y despejamos el valor de x, lo hacemos paso a paso:

