Formación de imágenes en los dioptros esféricos
Es sumamente sencillo basta que tengas en cuenta dos detalles es suficiente:
1) Debes tener en cuenta los puntos donde se hallan los focos; cuanto mayor es el índice de refracción más alejado del vértice del dioptrio se encuentra.
2) Con dos rayos de luz procedentes del objeto son suficientes para formar la imagen: a) el que sale paralelo al eje óptico en el primer medio y refractado pasa por el foco del segundo medio; b) el que procedente también del objeto pasando por su foco incide en la superficie esférica y refractado, se desplaza paralelamente al eje óptico en el segundo medio.
En el punto donde se cortan los rayos queda situada la imagen.
Dioptrios esféricos convexos:
n1<n2

El rayo que sale paralelo al eje óptico al penetrar en el medio con mayor índice de refracción tiende a juntarse con la normal pasando por el foco del segundo medio.
La normal en un punto de circunferencia además de ser perpendicular a la recta tangente en ese punto de la curva, pasa por el centro.
Dioptrios esféricos convexos:
n1>n2
Si el primer medio es el de mayor índice de refracción debes tener en cuenta las prolongaciones de los dos rayos de luz después de refractarse y recuerda que el foco se separa más del vértice de la superficie esférica cuanto mayor sea el índice de refracción:

Observarás que el rayo refractado al entrar en un medio de menor índice de refracción tiende a separarse de la normal y su prolongación pasa por el foco F’.
Recuerda que la normal en un punto de circunferencia pasa por su centro.
Lo mismo sucede con el rayo que sale del objeto y tiende a pasar por foco del medio de menor refracción su prolongación se desplaza horizontalmente respecto al eje óptico en el medio de mayor índice de refracción.
Donde ambas prolongaciones se cortan queda definida la imagen.
Dioptrios esféricos cóncavos:
n1<n2
Tenemos en cuenta el rayo que sale del objeto paralelo al eje principal y al entrar en un medio más refringente se acerca más a la normal pero su prolongación pasará por el foco del medio de donde salió.
El otro rayo tiende a pasar por el foco del medio más refringente pero su prolongación (en el medio menos refringente) se cortará con la prolongación del rayo anterior quedando determinada la imagen:

Dioptrios esféricos cóncavos:
n1 >n2
En la siguiente figura observamos que el rayo que sale paralelo al eje óptico de refracta al llegar al medio menos refringente separándose de la normal y pasa por el foco F’.
El otro rayo pasa por F y al incidir en la superficie esférica del dioptrio y refractado se desplaza en el segundo medio paralelo al eje óptico.
En el punto de encuentro de estos dos rayos refractados se fija la imagen:

5.35 Un objeto de 10 cm de altura se halla a 60cm de un dioptrio esférico convexo de Radio 20cm. Los índices de refracción valen
n1=1 y n2=1,5.
1) Las distancias focales.
2) Distancia a la que se forma la imagen.
3) Tamaño de la imagen.
Respuestas: 1ª) -40cm y 60cm; 2ª) 180cm; 3ª) -20cm
Hacemos una sencilla figura donde fijamos las distintas variables que nos van a permitir el cálculo a partir de las fórmulas estudiadas:

1) Calculamos las distancias focales a partir de la fórmula y haciendo sustituciones y operaciones obtenemos:

Es interesante que observes que se cumple lo estudiado: f + f’ = R
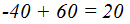
2= La distancia s’ entre imagen y vértice del dioptrio la calculamos de:

Sustituimos valores y hacemos operaciones:

Aumento lateral = 
Sustituimos valores y hacemos operaciones:

El signo menos nos indica que la imagen está boca abajo o invertida.
5.36 En el problema anterior la imagen, en valor absoluto, es mayor que el objeto ¿puede ser menor?, ¿puede ser igual?
Respuesta: Sí
Solución
Si el objeto lo colocas de modo que la distancia, en valor absoluto, s < f la imagen es mayor que el objeto y es virtual (está formado por las prolongaciones):

En el caso de que en valores absolutos, s y f sean iguales ni los rayos de luz refractados ni sus prolongaciones se cortan por ser líneas paralelas… “la imagen la encontrarás en el infinito”:

Analizamos ahora en el caso de s > f (tenemos en cuenta sus valores absolutos):

La imagen es real e invertida (su valor es negativo por ser ordenada en un eje de coordenadas y bajo cero).
5.37 Un objeto se halla a 40cm delante del vértice de un dioptrio esférico cóncavo de 20cm de Radio.
¿Cuál es la posición de la imagen si los índices de refracción valen n1=1 y n2=1,5?
Respuesta: -30cm
Hacemos el dibujo:

No tienes más que tomar la fórmula más adecuada que podría ser:

Sustituimos valores y hacemos operaciones:

5.38 Con los datos del problema anterior calcula la posición de la imagen pero esta vez considerando que el dioptrio es convexo y que su radio vale 30cm.
Respuesta: -180cm
Solución
Al ser convexa la superficie esférica, el Radio es positivo por lo que el resultado lo obtenemos de:

