Ecuaciones paramétricas de la recta
2.- Ecuaciones paramétricas de la recta
A partir de un punto de la recta y de su dirección podemos definir la ecuación de la recta.
Conocemos un punto de la recta  y por otra parte sabemos que la recta es paralela al vector
y por otra parte sabemos que la recta es paralela al vector  cuyas coordenadas son
cuyas coordenadas son  .
.

Vamos a seleccionar un nuevo punto cualquiera de la recta p(x,y).

Vemos que entre el punto inicial y este nuevo punto queda definido un vector  situado dentro de la recta, cuyas coordenadas serán (x-x1, y-y1).
situado dentro de la recta, cuyas coordenadas serán (x-x1, y-y1).

Como este vector es paralelo al vector 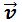 debe cumplir que sus coordenadas sean proporcionales.
debe cumplir que sus coordenadas sean proporcionales.
Luego:

Este sistema de ecuaciones se denomina ecuaciones paramétricas de la recta y el valor k se denomina parámetro de la ecuación; k puede ser cualquier valor (si tomamos un valor pequeño el punto p2 estará muy cerca del punto inicial p1, mientras que si tomamos un valor más alto el punto estará más alejado).

En el plano cartesiano está representada la recta "r" de la que conocemos el punto P1(-2, -3). Esta recta es paralela al vector 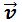 (4,3).
(4,3).
Luego desarrollando el sistema de ecuaciones paramétricas de esta recta tendríamos:

Para obtener nuevos puntos de la recta le daremos valores al parámetro de ecuación "k".

Luego las coordenadas del punto P2 son (2,0).

Luego las coordenadas del punto P3 son (6,3).
Vamos a representar estos dos nuevos puntos en el plano:

Hemos comprobado como los puntos calculados utilizando la ecuación paramétrica pertenecen a la recta.


