Parámetros Estadísticos
Para resumir la información obtenida de la muestra se calculan una serie de indicadores, llamados parámetros, que permiten sintetizar la información.
a) Parámetros de centralización: indican el valor central representativo de la distribución.
b) Parámetros de posición: una vez ordenada la distribución de menor a mayor, agrupa los elementos de la muestra en diversos grupos de igual tamaño.
c) Parámetros de dispersión: indican cómo de agrupados o dispersos se encuentran los elementos de la distribución.
a) Parámetros de centralización:
a.1.- Media aritmética: representa el valor medio que toman los datos de una observación estadística. Se calcula sumando todos los resultados y dividiendo la suma entre el número de registros. La media aritmética tan sólo se puede calcular con datos numéricos (no se puede calcular con datos cualitativos).
Por ejemplo, en nuestro ejemplo sumaríamos las 100 estaturas obtenidas. La suma la dividiríamos entre 100.
Media = suma de estaturas / 100 = 172,070 / 100 = 1,7207 m
La suma de estaturas también se podría calcular multiplicando el valor de cada observación por su frecuencia absoluta.
Cuando se utilizan intervalos de clase para calcular la meda aritmética se toma la marca de clase de cada intervalo y se multiplica por su frecuencia absoluta, dividiendo el resultado entre el número total de observaciones.
Media =(marca de clase * frecuencia absoluta) / 100 = 172,2 /100 = 1,722
Podemos ver que hay una ligera diferencia con el cálculo anterior ya que el utilizar intervalos de clase conlleva cierta simplificación de la información y por lo tanto cierto error.
a.2.- Moda: es el resultado más repetido en una observación estadística, es decir aquel que tiene mayor frecuencia absoluta (se puede calcular con datos numéricos y cualitativos).
En nuestro ejemplo la moda es la estatura 1,72 (se ha repetido 9 veces)
Puede haber más de una moda si resulta que hay distintos valores de la variable que coinciden en presentar la mayor frecuencia absoluta.
Si se trabaja con intervalos de clase, aquel intervalo con mayor frecuencia se denomina clase modal.
Vemos en nuestro ejemplo que cuando aplicamos intervalos de clase la clase modal es el intervalo 1,81 – 1,85 que presenta 17 repeticiones.
a.3.- Mediana: es el valor que toma la variable de manera que al ordenarlas de menor a mayor quedaría justo en el centro, siendo el 50% de los registros menores que ella y el otro 50% superiores a ella. La mediana sólo se puede calcular con variables cuantitativas.
En nuestro ejemplo al ordenar las observaciones de menor a mayor, el 43% de las observaciones son menores o iguales a 1,71. Si pasamos a la siguiente medida 1,72, el 52% de las observaciones son menores o iguales a dicha medida. Luego la mediana se sitúa en este valor (de las 9 veces que se repite hay una de ellas que deja por debajo el 50% de las observaciones y por encima el otro 50%).
Si se trabaja con intervalos de clase, la mediana se calcula aplicando la siguiente fórmula:
M = L0 + ((n/2 - F-1) * Am / Fm)
Siendo:
L0: extremo inferior de la clase mediana
n: tamaño de la muestra
F-1: frecuencia absoluta acumulada del intervalo de clase anterior
Am: Amplitud del intervalo de la clase mediana
Fm: frecuencia absoluta de la clase mediana
En nuestro ejemplo: la mediana se sitúa en el intervalo 1,71 – 1,75. Hasta el intervalo anterior se acumulaba el 40% de las observaciones; con el intervalo 1,71 – 1,75 pasamos a tener el 56% de las observaciones.
Vamos a calcular la mediana:
L0: 1,71
F-1: 40
Fm: 16
Luego:
M = L0 + ((n/2 - F-1) * Am / Fm)
M = 1,71 + ((100/2 - 40) * 5 / 16) = 1,741
b) Parámetros de posición:
b.1.- Cuartiles
Se ordenan las observaciones de menor a mayor y se dividen en 4 grupos, de forma que cada grupo reúna el 25 por ciento de la muestra. Los cuartiles son precisamente los valores de la variable que separan un grupo del siguiente.
Hay 3 cuartiles:
Q1 (cuartil inferior): es aquel valor que marca el límite superior del primer grupo. De él hacia abajo se concentra el 25% de los valores de la muestra.
Q2 (cuartil medio): es aquel valor que marca el límite superior del segundo grupo. De él hasta el primer cuartil se concentra el 25% de los valores de la muestra; y de él hasta el comienzo de la muestra se concentra el 50 por ciento de la muestra. El cuartil medio coincide con la mediana.
Q3 (cuartil superior): es aquel valor que marca el límite superior del tercer grupo. De él hasta el segundo cuartil se concentra el 25% de los valores de la muestra; y de él hasta el comienzo de la muestra se concentra el 75 por ciento de la muestra.
La diferencia entre el tercer cuartil y el primer cuartil (Q3 – Q1) se denomina rango intercuartílico y concentra el 50% de los valores de la muestra.
Volvemos al ejemplo de la estatura de los habitantes de una ciudad en la que tenemos 100 observaciones. Los cuartiles son:
Q1 = 1,62
Q2 = 1,72
Q3 = 1,81
c) Parámetros de dispersión:
Las medidas de dispersión son una serie de indicadores que nos informan si los datos de la muestra están próximos entre sí o si por el contrario están dispersos.
Estos parámetros se clasifican a su vez en 2 grupos:
c.1.- Parámetros de dispersión absoluta.
c.2.- Parámetros de dispersión relativa.
c.1.1.- Desviación media: mide la distancia media que hay entre todos los valores de la muestra y la media aritmética.
Cuando mayor sea la desviación media, mayor es la dispersión de la muestra, los datos están más separados; en cambio si el valor de la desviación es reducido significa que los valores están muy concentrados.
Desviación media = å |x1 – Media| / Nº de datos
X1 representa cada valor de la muestra.
| X1 – Media| las barras laterales indican que la diferencia entre cada valor de la muestra y la media se mide en valor absoluto, es decir, no se tiene en cuenta si es positiva o negativa.
A continuación vemos 2 ejemplos de una muestra de 12 datos. Ambas tienen la misma media, en cambio la desviación media de la segunda es significativamente mayor debido a que los valores de dicha muestra están más dispersos.

c.1.2.- Rango o recorrido: mide la diferencia entre el valor mayor y el valor menor de la muestra.
Mientras mayor sea el rango más dispersos están los valores.
En el primer ejemplo anterior, el valor máximo es 60 y el valor mínimo 40.
Rango = 60 – 40 = 20
En el segundo ejemplo anterior, el valor máximo es 91 y el valor mínimo 9.
Rango = 91 – 9 = 82
c.1.3.- Varianza
Al igual que la media, la varianza es un indicador que se utiliza para medir la dispersión (a mayor varianza, mayor dispersión), dando una información más precisa que la media.
Se calcula como suma de las diferencias al cuadrado de cada valor respecto a la media de la muestra, dividida ente el número de datos. La varianza se suele representar con la letra V.
V = (x1 – Media)2 / Nº de datos
Volvemos al ejemplo de las 2 muestras con 12 observaciones y calculamos sus varianzas.
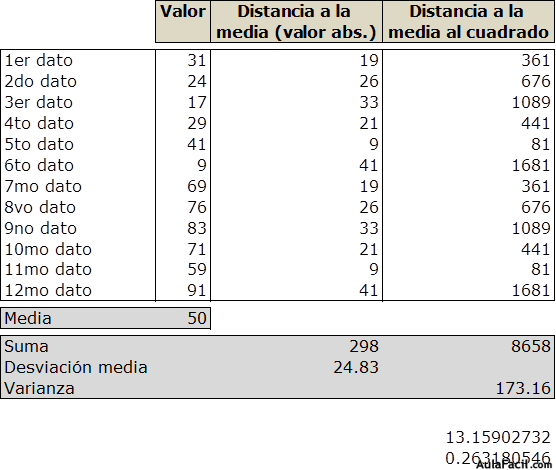
c.1.4.- Desviación típica
La desviación típica es otra medida de dispersión y se calcula como raíz cuadrada de la varianza. Es la medida de dispersión que más se utiliza.
s = √ Varianza
Calculamos la desviación típica de los dos ejemplos anteriores:
1er ejemplo: s = √ 42,50 = 6,519
2do ejemplo: s = √ 173,16 = 13,159
Dos distribuciones con la misma media, aquella que tenga una desviación típica mayor significa que tiene mayor dispersión, sus valores están más separados entre sí.
c.2.- Parámetros de dispersión relativa
c.2.1.- Coeficiente de variación de Pearson
La desviación típica es la unidad de dispersión que más se utiliza pero presenta un inconveniente: si dos distribuciones tienen medias diferentes sus desviaciones típicas no son directamente comparables.
Para poder comparar el nivel de dispersión de estas distribuciones se utiliza el coeficiente de variación de Pearson:
CV = s / Media
El CV de dos distribuciones es directamente comparable aunque tengan distintas medias. Aquella distribución con mayor CV tiene mayor dispersión.
Este coeficiente se suele presenta como % (el dato calculado se multiplica por 100).
Mientras menor sea el coeficiente de variación de Pearson significa que la dispersión de la muestra es menor lo que implica que la media de la muestra sea más representativa.
1er ejemplo: CV = 6,519 / 50 = 0,130
2do ejemplo: CV = 13,159 / 50 = 0,263
c.2.2.- Coeficiente de apertura
El coeficiente de apertura CA es el cociente entre el valor máximo de la muestra y el valor mínimo.
1er ejemplo: CA = 60 / 40 = 1,50
2do ejemplo: CA = 91 / 9 = 10,11
Mientras mayor es la apertura mayor es la dispersión de la muestra.
c.2.3.- Recorrido relativo
El recorrido relativo Rr de una muestra se calcula dividiendo el recorrido de la misma entre su media.
1er ejemplo: Rr = 20 / 50 = 0,40
2do ejemplo: Rr = 82 / 50 = 1,54
Al igual que en el caso anterior, mientras mayor es el recorrido relativo mayor es la dispersión de la muestra.


