Vectores en el plano cartesiano
1.- Coordenadas de un vector
Las coordenadas de un vector  vienen definidas por su punto inicial y su punto final.
vienen definidas por su punto inicial y su punto final.
 vienen definidas por su punto inicial y su punto final.
vienen definidas por su punto inicial y su punto final.
Las coordenadas del vector son:


Las coordenadas de este vector son:

Veamos otro ejemplo:
Tenemos el vector  cuyo punto de origen es P1 y punto final en P2
cuyo punto de origen es P1 y punto final en P2
 cuyo punto de origen es P1 y punto final en P2
cuyo punto de origen es P1 y punto final en P2
Luego las coordenadas del vector 

Podemos comprobar que el vector 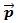 es equipolente a otro vector con origen en el punto (0,0) y final en el punto (-8,-2).
es equipolente a otro vector con origen en el punto (0,0) y final en el punto (-8,-2).
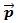 es equipolente a otro vector con origen en el punto (0,0) y final en el punto (-8,-2).
es equipolente a otro vector con origen en el punto (0,0) y final en el punto (-8,-2).2.-Vector de posición
Cualquier punto del plano cartesiano viene identificado por un vector libre diferente con inicio en el origen de coordenadas (0,0) y final en dicho punto. Este punto se denomina vector de posición.

Podemos ver que son diferentes porque se diferencian en el módulo, en la dirección o en el sentido.
Podemos ver como las coordenadas de cada vector posición coinciden con las coordenadas del punto que identifican.


3.- Vector de posición como combinación lineal
Vamos a definir dos vectores libres unitarios  con origen en el punto de corte de los ejes de abscisas y ordenadas (0,0), con la dirección de estos ejes respectivamente y con sentido positivo.
con origen en el punto de corte de los ejes de abscisas y ordenadas (0,0), con la dirección de estos ejes respectivamente y con sentido positivo.
 con origen en el punto de corte de los ejes de abscisas y ordenadas (0,0), con la dirección de estos ejes respectivamente y con sentido positivo.
con origen en el punto de corte de los ejes de abscisas y ordenadas (0,0), con la dirección de estos ejes respectivamente y con sentido positivo.
Las coordenadas de estos vectores son:

Cada vector de posición se puede definir como una combinación lineal de estos dos vectores.
Veamos un ejemplo:
Señalamos en el plano cartesiano el punto P1 (5,3) identificado por un vector de posición.
 =(5,3)
=(5,3)
Este vector lo podemos escribir como combinación lineal de 



Ya que:

Veamos otro ejemplo:

El vector  viene definido por la combinación lineal:
viene definido por la combinación lineal: 
 viene definido por la combinación lineal:
viene definido por la combinación lineal: 

4.- Vectores con igual dirección
Dos vectores  tienen la misma dirección (son paralelos) cuando sus coordenadas son proporcionales.
tienen la misma dirección (son paralelos) cuando sus coordenadas son proporcionales.
 tienen la misma dirección (son paralelos) cuando sus coordenadas son proporcionales.
tienen la misma dirección (son paralelos) cuando sus coordenadas son proporcionales.
Veamos un ejemplo:

Hemos dibujado dos vectores paralelos. Podemos comprobar como cumple con la propiedad indicada.



