Teoría: Definición

La derivada de una función en un punto mide la velocidad a la que varía el valor de la función en dicho punto al cambiar el valor de la variable independiente.

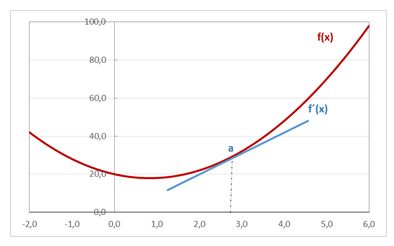
La derivada es igual a la pendiente de la recta tangente a la función en dicho punto.

Si nos fijamos en el gráfico siguiente la pendiente de la tangente es igual:

Mide lo que se incrementa “y” (variable dependiente) cuando se incrementa la variable independiente “x”.

Si el intervalo considerado (incremento de x) fuera cada vez más pequeño la pendiente de la tangente se iría aproximando cada vez más al incremento de la función.

Por eso la derivada equivale al límite de la variación de la variable dependiente “y” cuando la variación de la variable independiente es cada vez menor (cuando el incremento de la variable independiente tiende a cero).

La función derivada (se representa f´(x)) es la función que nos da el valor de la derivada de la función f(x) para cada valor de “x”.

El proceso de calcular la función derivada de una función dada se denomina diferenciación y entra dentro del área de las matemáticas denominada cálculo infinitesimal.

Algunas funciones no tienen derivadas en todos o en algunos de sus puntos

Para que una función sea derivable en un punto tiene que ser continua en dicho punto, es decir que pequeños incrementos de la variable independiente produzca pequeñas variaciones de la variable dependiente. No obstante, el que una función sea continua no garantiza que sea derivable.

Una función es derivable en un punto x si su derivada existe en dicho punto; una función es derivable en un intervalo abierto si es derivable en todos los puntos del intervalo.

La derivada de una función puede ser asimismo derivable. La derivada de una primera derivada se denomina segunda derivada. También podría existir la tercera derivada y así sucesivamente. Este proceso se denomina derivación sucesiva.

Cuando una función tiene más de una variable independiente podemos hablar de la derivada parcial cuando derivamos la función respecto a una de las variables independientes (tratando al resto de variables independientes como si fueran constantes).