Racionalización de Denominadores.
Recuerda que se llama irracional al número que no puede expresarse con números enteros ni fraccionarios. Son números que su expresión decimal tiene infinitas cifras pero sin formar períodos.
Podemos decir que 0,5 es lo mismo que 
.
es lo mismo que 0,75.
Todos estos números son racionales, podemos escribirlos como enteros o fraccionarios.
Existen números que no podemos expresarlos de este modo, por ejemplo 
a estos números los llamamos irracionales porque si queremos escribir el valor de los mismos nunca podremos acabar de ir escribiendo decimales. No hay ningún número que multiplicado por sí mismo te dé 2, ni 3 ni 11, ni 13, …. La raíz cuadrada de estos números nunca acabarás de obtener.
Es conveniente que las fracciones cuyo denominador sea irracional lo convirtamos en racional. En otras palabras, al proceso de obtener fracciones que no tengan raíces en el denominador llamamos racionalización de radicales de los denominadores:
Ejemplo: 
.El denominador es un número irracional, por mucho que intentes calcular su valor verás que nunca acabas de hacer operaciones.
Sabemos que si multiplicamos o dividimos al numerador y al denominador de una fracción por un mismo número, su valor sigue siendo el mismo.
Para hacer racional el denominador 
lo más simple es que le multipliquemos por sí mismo: 
.
Pero para que no varíe el valor de la fracción hemos de multiplicarle también al numerador por 
.Podemos decir que: 
son iguales pero 
no tiene como denominador un número irracional.
10.76 Racionaliza:
Respuesta: 
.
10.77 Racionaliza:
Respuesta: 
.
Solución:
10.78 Racionaliza:
Respuesta: 
.
Solución:
Las operaciones las tienes desarrolladas paso a paso:
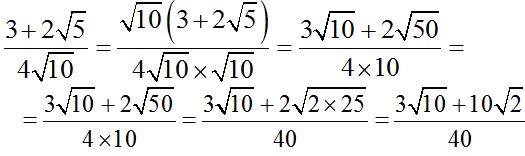
10.79 Racionaliza:
Respuesta: 
Solución:
El proceso de cálculos con letras es el mismo que aplicamos con los números.
Tienes desarrollado paso a paso la resolución del ejercicio:
10.80 Racionaliza:
Respuesta: 
.
Solución:
Tratamos ahora una raíz cúbica. Si tienes 
y quieres quitar la raíz tienes que conseguir que el exponente del radicando(que es 1) sea igual al índice de la raíz(que es 3). Para que sean iguales a 
tendrás que multiplicarle 
de este modo, en el denominador al multiplicar 
por 
tendrás que sumar los exponentes dejando la misma base: 
.
Para que el valor de la fracción no varíe tendrás que multiplicar también al numerador por 
:
10.81 Racionaliza:
Respuesta: 
.
Solución:
Para poder quitar la raíz de 
,5 tenía que tener como exponente un 7. Vemos que tendríamos que multiplicarle por 
de este modo al sumar los exponentes el valor obtenido iguala al índice de la raíz y entonces podemos simplificar. Para que no varíe el valor de la fracción tendremos que multiplicarle al numerador también por 
:
10.82 Racionaliza:
Respuesta: 
.
