Simplificación de Radicales. Raíz de Raíz.
Se trata de una sencilla operación muy útil en muchas circunstancias.
El valor de una raíz no varía si multiplicas o divides por un mismo número al índice y al exponente del radicando.
10.52 Simplifica:
Respuesta: 
Solución:
Al índice 21 y al exponente 7 podemos dividirles por 7 y sus cocientes serán 3 (nuevo índice) y 1 (nuevo exponente del radicando):
10.53 Simplifica:
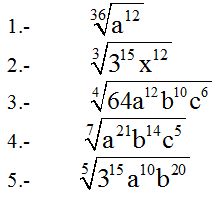
Respuestas:
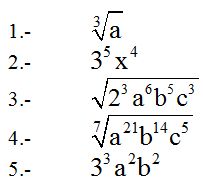
Soluciones:
1.- Paso a paso tenemos: 
2.- Cuando el cociente del índice es igual a 1, desaparece la raíz:
3.- Cuando simplifiques al índice y exponentes que haya dentro de una raíz debe ser el m.c.d de todos ellos por el que debas dividir a cada uno de ellos; en este ejercicio el número más grande capaz de dividir a 4, 6,12 y 10 es el 2:
¿Qué sucedería si hubiese otro factor con exponente: 1, 3, 5, 7?
Sencillamente, lo dejamos como está. Comprueba el siguiente ejercicio.
4.- 
: No existe un mismo número capaz de dividir a: 7, 21, 14 y 5 un número exacto de veces (siempre exceptuamos al 1). Si tuviésemos solamente los exponentes 7, 21 y 14 vemos que 7 es el m.c.d. de los tres pero como queda excluido el 5 no vale.
Basta que haya un solo exponente no divisible, para que NO podamos simplificar.
SUMAR Y RESTAR RADICALES .
10.54 Calcula: 
Respuesta: 
Solución:
Has de fijarte que los índices de todas las raíces y los radicandos sean iguales. En este ejercicio tenemos 9 veces positivas 
y 6 negativas. Es como si tuvieses 9 € - 6 € en que € = 
.
10.55 Calcula: 
Respuesta: 
Solución:
Hemos agrupado los términos semejantes y las hemos reducido separadamente.
10.56 Calcula:
Respuesta: 
Solución:
Como las dos raíces tienen el mismo índice restamos los radicandos. El denominador común es 
porque contiene a ambos denominadores.
Dividimos este denominador común entre el primer denominador y el cociente ‘b’ lo multiplicamos por su numerador.
Dividimos el denominador común entre el segundo denominador y el cociente ‘a’ lo multiplicamos por su numerador.
Como 
tiene raíz cuadrada exacta 
saldrá de la raíz, ab pero como denominador. Le pondremos 1 como numerador ya que no hemos podido sacar nada del numerador del radicando.
10.57 Calcula: 
Respuesta: 
Solución:
Observamos que en el segundo término 
podemos simplificar por 2 el índice y los exponentes del radicando quedándonos
.
Ahora veo que los dos términos son semejantes y ya puedo restarlos para ello, calculo la diferencia de la parte numérica conservando la parte literal.
10.58 Calcula: 
Respuesta: 
.
Solución:
La parte numérica de cada raíz descompongo en dos factores siendo uno de ellos cuadrado:
Saco fuera de la raíz los factores que tienen raíz cuadrada exacta y reduzco los términos semejantes:
10.59 Halla la respuesta de 
Respuesta: 
.
Solución:
Observo que lo que está dentro de la raíz tiene 3 términos. Dos de ellos son cuadrados perfectos, el otro término tiene signo menos y eso me da la pista para ver si se trata del cuadrado de la diferencia de dos números.
Hallo la raíz cuadrada de los términos que son cuadrados, pongo el signo menos entre ellos y esa diferencia la elevo al cuadrado sabiendo que la raíz cuadrada de
es 2a y la de 
es 3b.
10.60 ¿Crees que la fracción 
es igual a la fracción 
?
Contesta sí o no razonando el por qué.
Respuesta: Sí
Solución:
Te basta recordar que si al numerador y denominador de una fracción le multiplico por un mismo número, el valor de la fracción no varía: al numerador y denominador de la fracción 
multiplico por 3 y obtengo 
. Las dos fracciones tienen el mismo cociente exacto que es 2.
Lo mismo sucede con 
, si al numerador y denominador les multiplico por ‘y’ tengo otra fracción igual 
.
10.61 ¿Crees que 
son iguales?
Respuesta: Sí
Solución:
Si al numerador y denominador de la fracción que se encuentra dentro la raíz les multiplico por ‘y’ obtengo:
Veo que del denominador que está dentro de la raíz pueda extraer fuera 3y y en el denominador no me queda nada más que un 1 que no se pone:
10.62 ¿Se pueden sumar 
y 
? En caso positivo calcula el resultado:
Respuesta: 
Solución:
Nos fijamos que en 
puedo multiplicar al numerador y denominador de la fracción que está dentro de la raíz por el denominador y después, saco fuera de la raíz lo que pueda:
Veo que actualmente ambos sumandos son semejantes porque sus partes literales son iguales lo que me permite sumar sus coeficientes:
RAÍZ DE RAÍZ.
Se trata de hallar la raíz de una raíz. Algo parecido hacíamos cuando teníamos que elevar una potencia a otra. Recordarás que multiplicábamos los exponentes:
En el caso de las raíces, multiplicamos los índices dejando la misma cantidad subradical: 
Al mismo resultado llegamos si a este ejemplo lo consideramos como potencia:
Recordamos que para escribir una raíz en forma de potencia escribimos el radicando elevado a un exponente cuyo numerador es el exponente del radicando (en el ejemplo, 5 tiene de exponente 1) y como denominador el índice de la raíz. A partir de aquí lo tratamos como si elevásemos una potencia a otra y llegamos al mismo resultado.
10.63 Calcula:
Respuesta: 
Solución
No te olvides de simplificar la raíz dividiendo el índice y exponentes de 1 radicando por un mismo número:
10.64 Calcula: 
Respuesta: 
Solución:
Primero introducimos dentro de la raíz quinta el radicando que está bajo la raíz cúbica: 
.
Recuerda que para introducir factores en un radicando multiplicamos los exponentes de cada factor fuera de la raíz por el índice. Como al entrar se encuentran con potencias de las mismas bases, sumamos exponentes:
10.65 Calcula: 
Respuesta: 
.
Solución:
Tienes resuelto paso a paso:
10.66 Halla el valor de:
Respuesta: 
10.67 Halla el valor de: 
Respuesta: 
.
