Estadística Básica
El histograma aporta indicaciones sobre la forma de la distribución, la posición central y la dispersión, pero de manera aproximada. Para estudiar con más detalle una distribución, los parámetros estadísticos utilizados más habitualmente son la media aritmética, el recorrido y la desviación típica.
Media aritmética (X ). Es el resultado medio de los valores obtenidos.

donde 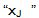 son los valores obtenidos en la muestra y “n” es el número de resultados.
son los valores obtenidos en la muestra y “n” es el número de resultados.
Es decir:

En el caso de series clasificadas, como las reflejadas en histogramas, se puede calcular la media, de la siguiente forma:

donde:
c = número de clases diferentes (número de resultados diferentes obtenidos en la tirada de dados o número de medidas de diámetro diferentes encontradas en los tubos).
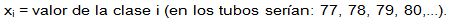

En el ejemplo de los diámetros de tubos, la media se calcularía de la siguiente forma:

Recorrido (R). Es la diferencia entre el valor más grande y el valor más pequeño obtenidos.
En el ejemplo de los diámetros de tubos, el recorrido seria:
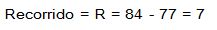
Desviación típica 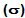 . Es la distancia media de los puntos de la distribución con respecto al valor medio. Para las series clasificadas, como las reflejadas en histogramas, se calcula con la siguiente fórmula:
. Es la distancia media de los puntos de la distribución con respecto al valor medio. Para las series clasificadas, como las reflejadas en histogramas, se calcula con la siguiente fórmula:

En el ejemplo del diámetro de tubos, la desviación típica sería:

Visualizando sobre el histograma la media, el recorrido y la desviación típica, se obtendría:
HISTOGRAMA CON MEDIA, RECORRIDO Y DESVIACIÓN TÍPICA

VARIABILIDAD DE UN PROCESO
Un proceso no se desarrolla necesariamente del mismo modo, ni produce siempre los mismos resultados, sino que está sujeto a variaciones. A esta circunstancia se le denomina variabilidad del proceso.
La variabilidad es una característica permanente en todo proceso. El control estadístico del proceso (S.P.C.), sin suprimir la variabilidad, permite preverla y disminuirla.
El conjunto de causas que provocan la variabilidad de un proceso se puede dividir en dos tipos:
- Causas asignables. Son aquellas que pueden ser identificadas y reparadas. Hay posibilidad de actuar para suprimirlas. Sus efectos son puntuales y provocan variaciones importantes en el proceso. Ejemplos de causas asignables: un cambio de materias primas, un cambio de operario, una intervención de mantenimiento, la modificación de un reglaje de máquina. Estas causas provocan variaciones en el proceso, pero se pueden suprimir. Para ello es necesario identificarlas, averiguar sus efectos y poner en marcha las medidas correctoras oportunas.
- Causas aleatorias. Son aquellas que es posible reducir, pero no pueden ser eliminadas del proceso. Son numerosas e independientes entre sí. Ejemplos: pequeñas modificaciones de las condiciones ambientales, variaciones imperceptibles en la alimentación eléctrica.
Todo parámetro de un proceso en el que sólo existan causas aleatorias sigue una ley normal o distribución normal.
Una distribución normal está caracterizada por la media y la desviación típica, de forma que:
- 1s = 66,26% de los datos analizados.
- 2s = 95,44% de los datos analizados.
- 3s = 99,73% de los datos analizados.
- 4s = 99,944% de los datos analizados.
La distribución normal, también llamada campana de Gauss, tiene la siguiente representación:
DISTRIBUCIÓN NORMAL

Uno de los objetivos del control estadístico del proceso es conseguir eliminar todas las causas asignables, de manera que la representación de sus parámetros siga una distribución normal.
LOS GRÁFICOS DE CONTROL
Un gráfico de control es una representación de la evolución de una característica en el tiempo. Esta característica puede ser representativa de la calidad del producto o del proceso, y se mide o se calcula a partir de una muestra.
En el gráfico se encuentra la línea central, que representa la inedia de los valores de la característica cuando el proceso es estable, la línea de control superior y la línea de control inferior. Estos límites son el reflejo de la variabilidad natural del proceso (la debida a causas aleatorias).
GRÁFICO DE CONTROL

Si un punto está fuera de los límites de control, se dice que el proceso es inestable, o que está fuera de control. Pero un proceso también puede ser inestable aunque todos sus puntos estén dentro de los límites. Esto ocurre cuando los puntos no se distribuyen de forma aleatoria entre los límites de control.
Cuando esto ocurre, quiere decir que sobre el proceso están actuando causas asignables, por lo que es preciso tomar medidas para identificarlas y eliminarías.
Los casos más habituales de procesos inestables son los siguientes:
- Secuencia. Serie de 8 puntos consecutivos por encima o debajo de la media.
- Tendencia. Serie de 7 puntos consecutivos crecientes o decrecientes.
- Periodicidad. La posición de los puntos asciende o desciende de forma cíclica.
