Método de transporte
Es un método determinístico que en general se refiere literalmente a la distribución de cualquier bien desde cualquier grupo de centros de abastecimiento llamados Orígenes a cualquier grupo de centros de recepción llamados Destinos de tal manera que se inicia la búsqueda de los costos totales de distribución. Puede describirse en la forma de una matriz con transporte de un lugar a otro.
Supóngase, por ejemplo, que se tienen transportes de fábricas a almacenes, con las fábricas representadas por renglones, y almacenes por las columnas de la matriz. En la figura 11 se tienen tres fábricas y cuatro almacenes. Cada celda en la matriz representa una ruta de una fábrica en particular a un almacén específico. En el ejemplo existen 12 rutas posibles.
El lado derecho de la matriz se indican las cantidades disponibles en cada fábrica. Estas cantidades deben transportarse a uno o más almacenes. En la parte inferior de la matriz se indican las partes requeridas en cada almacén. Estas cantidades requeridas deben suministrarse desde una o más fábricas. Por el momento, se supone que la cantidad total disponible de todas las fábricas es igual al total de las cantidades requeridas en todos los almacenes.
El objetivo del problema del transporte es encontrar las rutas de transporte de las fábricas a los almacenes que minimizaran el costo total del transporte. En cada celda a matriz se indica el costo unitario por transporte de una unidad a través de la celda o ruta. El costo total del transporte es entonces la suma de las cantidades embarcadas a través de cada celda multiplicada por los costos unitarios de transporte a través de esa celda.


Para describir matemáticamente el problema del transporte, sea:
Xij = Cantidad transportada de la fabrica i al almacén j
Cij = Costo unitario por transporte de la fabrica i al almacén j
Entonces en costo total de transporte es

Donde “m” es el número de fábricas y “n” es el número de almacenes.
Desean encontrarse los valores de Xij que minimizaran el valor de C sujeto a los límites:
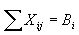
El transporte total de cada almacen j debe ser igual a la cantidad requerida en el almacen.

La cantidad total transportada de cada fábrica “i” debe ser igual a la cantidad disponible en la fábrica, en donde Xij debe ser mayor que cero, matemáticamente queda plasmado así:
Xij ³ 0